DIMA - Teorie grafů



Barevnost grafu

Teorie ⇫

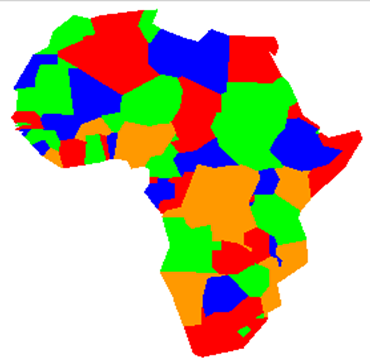
Poprvé je problém barvení grafů zmiňovám v roce 1840 a poté opět v roce 1852 ve spojení s obarvením politické mapy Anglie. Tehdy Frederic Guthrie poukázal na to, že je možné tuto mapu obarvit pouze čtyřmi barvami. Že se nejedná o jednduchý problém svědčí to, že o důkaz této teorie se pokoušeli matematici od roku 1860, ale teprve až v roce 1976 američtí vědci za pomoci počítače. Nicméně ani tento důkaz není některými matematiky stále uznán.

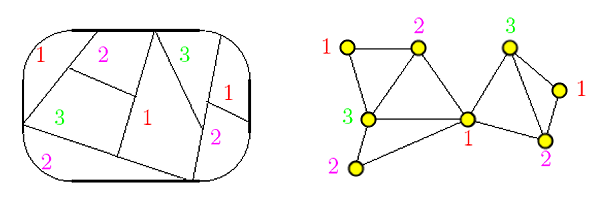
Barvení map lze převést na barvení rovinných grafů tak, že jednotlivé vrcholy grafu představují státy a hrany pak společné hranice mezi nimi.

Čtyřbarevná mapa

Definice obarvení grafu:

Obarvením grafu G pomocí k barev myslíme libovolné zobrazení c:V(G)→{1,2,3,...,k} takové, že každé dva vrcholy spojené hranou dostanou vzájemně různé barvy, tj. c(u)≠c(v) pro všechny {u,v}∈E(G).

Poznámka: Čísla 1,2,3,...,k z předchozí definice nazýváme barvami vrcholů, je to pohodlnější, než popisovat barvy běžnými jmény, jako bílá, červená, ... .

Definice barevnosti:

Barevnost grafu G je nejmenší přirozené číslo, označujeme ho χ(G) - chromatické číslo, pro které existuje obarvení grafu G pomocí χ(G) barev.

barvení map

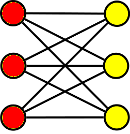
Poznámka: Každý bipartitní graf , má barevnost menší nebo rovnu dvěma.

Bipartitní graf

Věta (Problém čtyř barev):

Barevnost každého rovinného grafu je ≤4.

Příklad

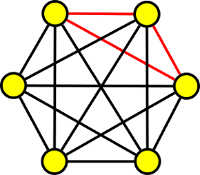
Nechť G je graf získaný z kompletního grafu K6 odebráním hran tvořících K3 v K6. Určete chromatické číslo grafu G.

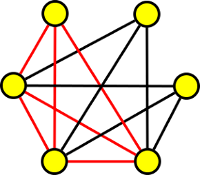graf K6 graf K6-K3
graf K6 graf G

V grafu se nachází K4, tedy čtyři barvy jsou nutné. Zbylé dva vrcholy už dobarvit dokážeme. Graf G má tedy chromatické číslo 4.

Platí následující tvrzení:

Tvrzení:

Nechť G je graf na n vrcholech. Pak χ(G)≤n a rovnost nastává právě, když G≅Kn je úplný graf.

Tvrzení:

Graf G má barevnost 1 právě když nemá žádné hrany. Graf má barevnost 2 právě když nemá žádnou kružnici liché délky jako podgraf.

Řešený příklad ⇫

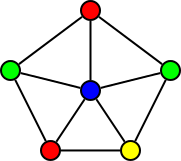
1. Určete a zdůvodněte barevnost tohoto grafu:

zadani

Krok 1

Vidíme, že obvodová kružnice tohoto grafu má délku 5, což je liché číslo, a proto je potřeba na její korektní obarvení použít alespoň tři barvy 1, 2, 3. Pak je ale středový vrchol spojený s každou z těchto barev 1, 2, 3, tudíž pro něj potřebujeme čtvrtou barvu 4.

Krok 2

vysledek

Krok 3

To znamená, že daný graf má barevnost 4.

2. Kolika nejvýše barvami obarvíme kompletní bipartitní graf, jestliže mu přidáme jednu hranu?

Krok 1

Z posledního tvrzení v teorii víme, že graf, který nemá kružnici liché délky (bipartitní graf je graf, který nemá kružnici liché délky), má barevnost 2.

Krok 2

Přidáme-li tedy do bipartitního grafu jednu hranu, musíme barevnost zvětšit o jednu, takže barevnost tohoto grafu bude 3.

Úlohy k řešení ⇫

1. Kolika nejméně barvami korektně obarvíte graf pravidelného osmistěnu?

test

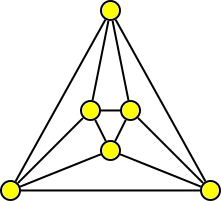
Výsledek

3

2. Kolik nejméně barev je třeba na dobré vrcholové barvení rovinného nakreslení graf K5-e?

Výsledek

4

3. Najdete rovinný graf, na jehož obarvení je potřeba alespoň 5 barev? Zdůvodněte.

Výsledek

takový graf neexistuje podle věty o 4 barvách

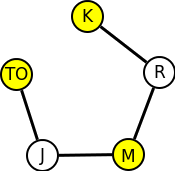
4. Podle předpisů se káva nesmí skladovat společně s rýží, rýže s moukou, mouka s jablky a jablka se nesmí skladovat společně s tropickým ovocem. Kolik nejméně místností je potřeba pro uskladnění všech druhů zboží?

Výsledek

stačí dvě místnosti (žlutá a bílá)

sklad

Zdroje textů

  1. DIMA - diskrétní matematika, http://oliva.uhk.cz
  2. Hliněný, Petr. Diskrétní Matematika (456-533 DIM), 2006
  3. Kovář, Petr. DISKRÉTNÍ MATEMATIKA a ÚVOD DO TEORIE GRAFŮ ( příklady k procvičení ), 2012
  4. Wikipedia, http://cs.wikipedia.org/wiki/Problém_čtyř_barev