Kostra grafu
Teorie ⇫
Definice kostry grafu:
Kostra grafu G=(V,E) je strom T=(V,E´), E´⊆E, tj. acyklický a souvislý faktor grafu G (≈ souvislý podgraf grafu G obsahující všechny jeho vrcholy, který neobsahuje kružnici).
Je to strom "rozpínající se" do všech vrcholů daného grafu (spanning tree). Jak dále uvidíme, v daném grafu může existovat více koster.
Poznámka: Vrcholové množiny G a T se shodují. Na výběr množiny E´ existují více možností, které jsou v souladu s definicí stromu.
Příklad grafu a všech jeho různých koster:

Z definice kostry bezprostředně vyplývá věta o existenci kostry v souvislém grafu:
- Důkaz ( Milková: Problém minimální kostry grafu):
Důkaz toho, že souvislý graf G obsahuje alespoň jednu kostru, provedeme indukcí podle počtu hran grafu G.
- Souvislý graf s jednou hranou je strom a jeho kostra je celý graf.
- Nechť věta platí pro graf s m hranami, m≥1. Její platnost dokážeme i pro graf s (m+1) hranami.
Nechť G=(V,E) je souvislý graf s (m+1) hranami. Jestliže graf G neobsahuje kružnici, pak graf G je strom a jeho kostra je rovna grafu G. Pokud graf G obsahuje alespoň jednu kružnici C, pak odebráním libovolné hrany e ležící na kružnici C získáme (dle tvrzení: Nechť graf G je souvislý a nechť obsahuje kružnici C. Pak graf G-e, kde e je libovolná hrana kružnice C, je také souvislý.) souvislý graf G-e, který má o jednu hranu méně než graf G. Podle indukčního předpokladu graf G-e obsahuje alespoň jednu kostru. Ta je zároveň kostrou grafu G.
Naopak, nechť graf G obsahuje alespoň jednu kostru. Pak graf G je souvislý, neboť mezi každými dvěma jeho vrcholy existuje alespoň ta cesta, která je totožná s právě jednou cestou mezi těmito vrcholy v kostře grafu G.∎
- Důsledek 1:
V souvislém grafu G=(V,E) platí vztah |E|≥|V|-1.
- Důkaz (Milková: Problém minimální kostry grafu):
Podle předchozí Věty 1 v grafu G existuje kostra H=(V,E´), |E´|≤|E| a podle věty (stromy – ekvivalentní podmínky) platí |E´|=|V|-1. Odtud |E|≥|E´|=|V|-1.∎
Důkaz Věty 1 dává návod, jak kostru grafu najít. Dokud v grafu existují kružnice, vyjímáme z libovolné kružnice libovolnou hranu, až dostaneme graf bez kružnic. Vyjmutím hrany z kružnice neporušujeme souvislost, tudíž výsledný graf je kostra původního grafu. Z vlastností stromů a definice kostry je ihned vidět, že k získání kostry daného grafu G=(V,E) bude nutné vyjmout |E|-(|V|-1)=|E|-|V|+1 hran.
- Věta 2:
Nechť je dán souvislý graf G=(V,E) a H=(V,E') jeho kostra. Pak pro každou hranu e={v,w}, e∈E-E', platí:
- Důkaz (Milková: Problém minimální kostry grafu):
Nechť e={v,w} je libovolná hrana grafu G, která neleží v kostře H. Graf (V,(E'∪{e}) je zřejmě souvislý a podle věty (stromy – ekvivalentní podmínky) obsahuje kružnici. Tuto kružnici tvoří cesta P z vrcholu v do vrcholu w obsažená v kostře H spolu s hranou e. Odebráním libovolné hrany e' cesty P dostaneme (dle tvrzení: Nechť graf G je souvislý a nechť obsahuje kružnici C. Pak graf G-e, kde e je libovolná hrana kružnice C, je také souvislý.) Souvislý graf H'=(V,(E'∪{e})-{e'}), který je, vzhledem k počtu vrcholů a hran, strom a obsahuje všechny vrcholy grafu G. To znamená, že graf H' je také kostra grafu G.∎
Právě dokázaná věta ukazuje, jak můžeme z jedné kostry grafu G získat jinou kostru tohoto grafu.

Z předchozího příkladu (na začátku) vyplývá, že graf G může mít více koster. Přirozená otázka je, kolik koster má daný graf G. Dvě kostry T1=(V,E1) a T2=(V,E2) považujeme za různé, když E1≠E2. Kostry mohou být navzájem izomorfní. Pro daný graf G označme symbolem t(G) počet jeho koster.
Ukážeme metodu, která tento počet umožňuje zjistit. Nejprve jsi vysvětlíme tyto operace:
identifikace dvojice vrcholů: dva vrcholy x a y jsou identifikované, když oba vrcholy jsou nahrazena novým vrcholem z tak, že všechny hrany v G incidentní s x a y jsou teď incidentní s vrcholem z. Když vznikne smyčka {z,z}, tak ji vynecháme.
Příklad identifikace vrcholů x a y:
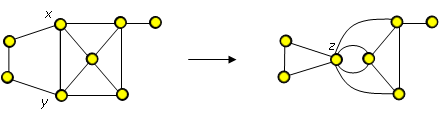
-
kontrakce hrany: pod kontrakcí hrany e={x,y} grafu G rozumíme operaci odebrání hrany e z grafu a následnou identifikaci jejich koncových vrcholů x a y. Nechť G=(V,E) je (multi)graf a e je jeho hrana, pak (multi)graf G/e nazýváme kontrakce (multi)grafu G podle hrany e. Když G je souvislý (multi)graf, pak i (multi)graf G/e je souvislý (multi)graf.
Příklad kontrakce hrany e:
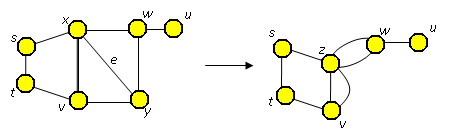
Teď ještě několik úvah:
- Důkaz (Milková: Problém minimální kostry grafu):
Nechť G=(V,E) je graf a C=(v0,e1,v1,e2,v2,...,ek,v0) kružnice délky k v grafu G. Pak (dle tvrzení: Nechť graf G je souvislý a nechť obsahuje kružnici C. Pak graf G-e, kde e je libovolná hrana kružnice C, je také souvislý.) je každý graf Hi=G-ei,i=1,2,...,k, souvislý, obsahuje všechny vrcholy a vzhledem k předpokladu neobsahuje kružnici, tudíž tvoří kostru grafu G.∎
- Důsledek 2:
Obsahuje-li souvislý graf p po dvou hranově disjunktních kružnic C1,C2,...,Cp, jejichž délky jsou postupně k1,k2,...,kp, pak obsahuje k1∙k2∙...∙kp koster.
- Důkaz (Milková: Problém minimální kostry grafu):
Protože kružnice jsou po dvou hranově disjunktní, stačí k získání kostry daného grafu zvolit, obdobně jako v důkazu Tvrzení 1, v každé kružnici jednu libovolnou hranu, kterou do kostry nezařadíme. Volit jednu z ki hran kružnice Ci, pro i=1,2,...,p, můžeme k1,k2,...,kp různými způsoby. Odtud dostáváme různých k1∙k2∙...∙kp koster.∎
Příklad
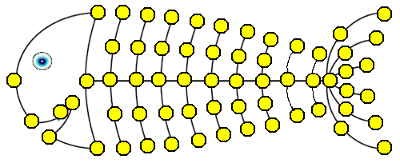
Kolik různých koster má tento graf?
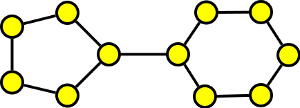
Podívejme se na kostru grafu takto – jaké hrany z grafy vymažeme, aby zbyl strom? Zajisté musíme vymazat některou hranu z první kružnice (5 možností) a některou hranu z druhé kružnice (6 možností). Na druhou stranu to v tomto jednoduchém příkladě už stačí, vždy pak zbude strom. Výběr vymazané hrany z první kružnice je nezávislý na druhé kružnici (jsou disjunktní), a proto dle principu nezávislých výběrů máme 5 · 6 = 30 možností vybrat dvě hrany k vymazání. Celkem tedy vyjde 30 koster.
Důkaz (Milkova: Problém minimální kostry):
Protože graf G obsahuje kostru, je graf G souvislý. Neexistence kružnice v grafu G plyne z Tvrzení 1, neboť kdyby alespoň jedna kružnice C v grafu G existovala, muselo by v grafu existovat alespoň tolik koster, kolik je hran ležících na kružnici C, což je zřejmě více než jedna a to by byl spor s předpokladem.∎
- Věta 3 (o počtu koster):
-
Nechť G je graf a e jeho libovolná hrana. Potom pro počet jeho koster t(G) platí:
t(G)=t(G-e)+t(G/e).
Použitím předcházející věty je možné počítat t(G) pro některé grafy na malém počtu vrcholů. Je možné postupovat například takhle:
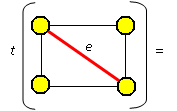
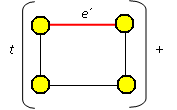
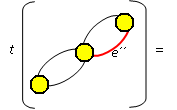
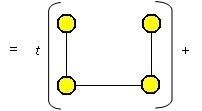
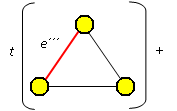
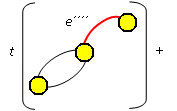

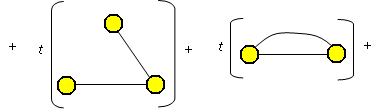

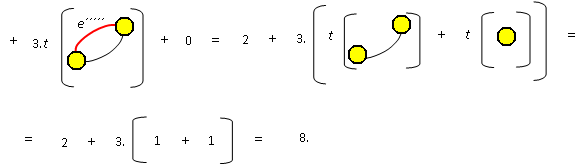
Kostry grafu jsou:

Následující věty hovoří o počtu koster některých speciálních grafů.
- Věta 4:
-
Počet koster úplného grafu Kn je nn-2.
Důkaz je možné najít v Milková, E.: Problém minimální kostry grafu. Gaudeamus, Hradec Králové, 2001
- Věta 5:
Úplný bipartitní graf K2,n obsahuje n∙2n-1 koster.
Důkaz je možné najít v Milková, E.: Problém minimální kostry grafu. Gaudeamus, Hradec Králové, 2001
- Věta 6:
-
Úplný bipartitní graf K3,n obsahuje n2∙3n-1 koster.
Důkaz je možné najít v Milková, E.: Problém minimální kostry grafu. Gaudeamus, Hradec Králové, 2001
Řešený příklad ⇫
1. Kolik různých koster má tento graf?

Krok 1
Jak vidíme graf má dvě kružnice, které nejsou hranově disjunktní, proto není možné použít Důsledek 2 (o počtu koster). Můžeme použít Větu 3 o počtu koster:
Krok 2

Krok 3
 = 8 (je to kružnice délky 8, použijeme Tvrzení 1)
= 8 (je to kružnice délky 8, použijeme Tvrzení 1)
 = 4∙4 = 16 (dvě hranově disjunktní kružnice, použijeme Důsledek 2)
= 4∙4 = 16 (dvě hranově disjunktní kružnice, použijeme Důsledek 2)
Krok 4
Celkový počet koster je tedy 8 + 16 = 24.
2. Kolik různých koster má tento graf?

Krok 1
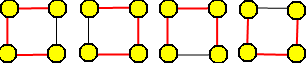
Graf si rozdělíme na jednotlivé hranově disjunktní podgrafy:
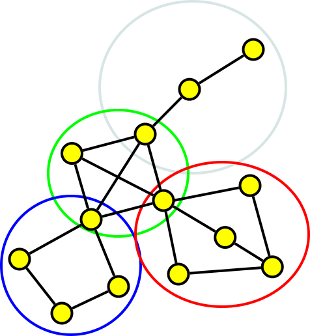
Krok 2
Tyto podgrafy mají tyto počty koster: 1, 42, 3∙22 a 4
Krok 3
Výsledný počet koster je tedy: 1∙16∙12∙4 = 768
Úlohy k řešení ⇫
1. Kolik různých koster má tento graf?

Výsledek
5
2. V grafu G určete počet koster, ketré se vyskytují v podgrafu indukovaném vrcholy {c,d,e,f,g,h}.
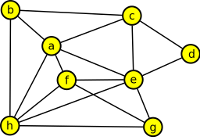
Výsledek
Výsledný počet koster je 3∙42 = 48
3. V doplňku následujícího grafu určete počet koster a jednu kostru nakreslete:
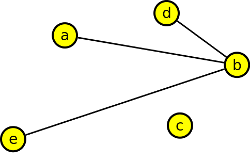
Výsledek
Počet koster je 1∙42
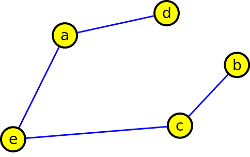
4. V grafu G určete počet koster, které se vyskytují v podgrafu indukovaném vrcholy {b,c,d,e,f,g,h}.
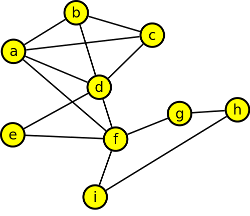
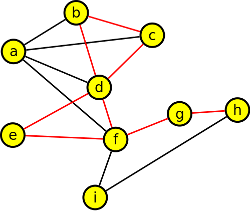
Výsledek
Počet koster je 3∙3∙1=9
5. Kolik hran je třeba vynechat z kompletního bipartitního grafu Km,n, aby zůstala kostra? (Podívejte se na Důsledek 1)
Výsledek
(mn)-(m+n-1) = mn-m-n+1 = (m-1)(n-1)
6. Na uvedeném grafu najděte libovlnou kostru a pak určete její centrum či bicentrum.
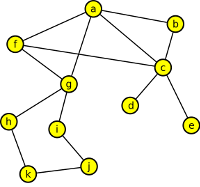
Výsledek
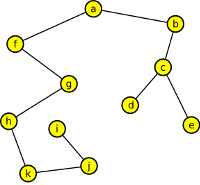
Bicentrum jsou vrcholy f,g
Zdroje textů
- DIMA - diskrétní matematika, http://oliva.uhk.cz
- Milková, E.. Problém minimální kostry grafu, Hradec Králové: Gaudeamus, 2001
- Hliněný, Petr. Diskrétní Matematika (456-533 DIM), 2006
- Kovář, Petr. DISKRÉTNÍ MATEMATIKA a ÚVOD DO TEORIE GRAFŮ ( příklady k procvičení ), 2012