Dijkstrův algoritmus
Teorie ⇫
Hledání nejkratší cesty z daného vrcholu do ostatních vrcholů v nezáporně hranově ohodnoceném grafu
Dijkstrův algoritmus je nejrychlejší známý algoritmus pro nalezení všech nejkratších cest ze zadaného uzlu do ostatních uzlů grafu, který neobsahuje hrany záporné délky.
Vzpomeňme si na Jarníkův algoritmus.
Předpokládejme, že jednotlivá ohodnocení hran v daném grafu odpovídají vzdálenostem mezi vrcholy daného grafu a uvažujme modifikaci: V každém kroku udržujeme pro každý vrchol x, který neleží v modrém stromu, aktuální informaci udávající nejkratší vzdálenost mezi vrcholem x a počátečním vrcholem v.
Touto modifikací dostáváme Dijkstrův algoritmus pro nalezení nejkratší cesty mezi daným vrcholem v a ostatními vrcholy v hranově nezáporně ohodnoceném grafu, který E.W.Dijkstra navrhl a popsal v roce 1950 v práci “A note on two problems in connection with graphs, Numer. Math.,1, 1959, pp. 269-271”.
Ilustrace obou algoritmů, Jarníkova a Dijkstrova
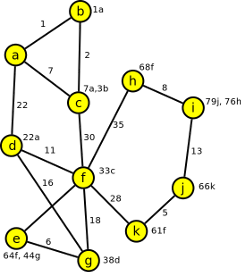
Budeme používat stejný graf, jako v případech pro hledání minimální kostry a to především pro ilustraci podobnosti s Jarníkovým algoritmem
Jarníkův algoritmus - nalezení minimální kostry
| a | b | c | d | e | f | g | h | i | j | k | |
| a | 1 | 7 | 22 | ||||||||
| b | 1 | 2 | |||||||||
| c | 7 | 2 | 30 | ||||||||
| d | 22 | 11 | 16 | ||||||||
| e | 31 | 6 | |||||||||
| f | 30 | 11 | 31 | 18 | 35 | 28 | |||||
| g | 16 | 6 | 18 | ||||||||
| h | 35 | 8 | 24 | ||||||||
| i | 8 | 13 | |||||||||
| j | 24 | 13 | 5 | ||||||||
| k | 28 | 5 |
| a | (0,a) | |||||||||
| b | (1,a) | |||||||||
| c | (7,a) | (2,b) | ||||||||
| d | (22,a) | (22,a) | (22,a) | |||||||
| e | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (31,f) | (6,g) | ||||
| f | (∞,a) | (∞,a) | (30,c) | (11,d) | ||||||
| g | (∞,a) | (∞,a) | (∞,a) | (16,d) | (16,d) | |||||
| h | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (35,f) | (35,f) | (35,f) | (35,f) | (24,j) | (8,i) |
| i | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (13,j) | |
| j | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (5,k) | ||
| k | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (28,f) | (28,f) | (28,f) |
- modré hrany, které tvoří minimální kostru zadaného grafu: {a,b},{b,c},{a,d},{g,e},{d,f},{d,g},{i,h},{j,i}, {k,j},{f,k}
Dijkstrův algoritmus - nalezení nejkratší vzdálenosti mezi vrcholem a a vrcholem h
| a | b | c | d | e | f | g | h | i | j | k | |
| a | 1 | 7 | 22 | ||||||||
| b | 1 | 2 | |||||||||
| c | 7 | 2 | 30 | ||||||||
| d | 22 | 11 | 16 | ||||||||
| e | 31 | 6 | |||||||||
| f | 30 | 11 | 31 | 18 | 35 | 28 | |||||
| g | 16 | 6 | 18 | ||||||||
| h | 35 | 8 | 24 | ||||||||
| i | 8 | 13 | |||||||||
| j | 24 | 13 | 5 | ||||||||
| k | 28 | 5 |
| a | (0,a) | |||||||||
| b | (1,a) | |||||||||
| c | (7,a) | (3,b) | ||||||||
| d | (22,a) | (22,a) | (22,a) | |||||||
| e | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (64,f) | (44,g) | ||||
| f | (∞,a) | (∞,a) | (33,c) | (33,c) | ||||||
| g | (∞,a) | (∞,a) | (∞,a) | (38,d) | (38,d) | |||||
| h | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (68,f) | (68,f) | (68,f) | (68,f) | (68,f) | (68,f) |
| i | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (79,j) | |
| j | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (66,k) | ||
| k | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (61,f) | (61,f) | (61,f) |
- nejkratší cesta mezi danými vrcholy je (a,b,c,f,h)
Příklad
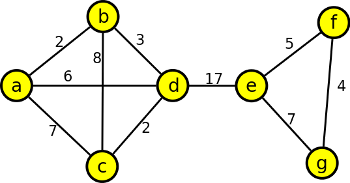
Najděte nejkratší cestu mezi vrcholy a a d pomocí Dijkstrova algoritmu. Graf nekreslete!
| a | b | c | d | e | |
| a | 2 | 2 | 2 | ||
| b | 2 | 1 | |||
| c | 2 | 1 | 2 | ||
| d | 2 | 1 | |||
| e | 2 | 1 |
Nejprve si pod sebe napíšeme všechny vrcholy počínaje výchozím vrcholem:
| a | |||||
| b | |||||
| c | |||||
| d | |||||
| e |
Potom do našeho zápisu doplníme vzdálenost jednotlivých vrcholů od vrcholu a a přes jaký vrchol jsme této vzdálenosti dosáhli. Pokud vzdálenost neznáme, zapíšeme ∞.
| a | b | c | d | e | |
| a | 2 | 2 | 2 | ||
| b | 2 | 1 | |||
| c | 2 | 1 | 2 | ||
| d | 2 | 1 | |||
| e | 2 | 1 |
| a | (0,a) | ||||
| b | (2,a) | ||||
| c | (2,a) | ||||
| d | (∞,a) | ||||
| e | (2,a) |
Dále pokračujeme z vrcholu b, protože máme volnou hranu o velikosti 1 incidentní s tímto vrcholem. Opět zapisujeme vzdálenost až z vrcholu a, tzn. že přičítáme hodnotu u vrcholu b. Pokud je ovšem vzdálenost přes vrchol b větší než původní vzdálenost, necháme původní hodnotu.
| a | b | c | d | e | |
| a | 2 | 2 | 2 | ||
| b | 2 | 1 | |||
| c | 2 | 1 | 2 | ||
| d | 2 | 1 | |||
| e | 2 | 1 |
| a | (0,a) | ||||
| b | (2,a) | (2,a) | |||
| c | (2,a) | (2,a) | |||
| d | (∞,a) | (∞,a) | |||
| e | (2,a) | (2,a) |
Opět pokračujeme stejným způsobem z dalšího vrcholu incidentního s další nejmenší hranou, tentokrát e.
| a | b | c | d | e | |
| a | 2 | 2 | 2 | ||
| b | 2 | 1 | |||
| c | 2 | 1 | 2 | ||
| d | 2 | 1 | |||
| e | 2 | 1 |
| a | (0,a) | ||||
| b | (2,a) | (2,a) | |||
| c | (2,a) | (2,a) | (2,a) | ||
| d | (∞,a) | (∞,a) | (3,e) | ||
| e | (2,a) | (2,a) | (2,a) |
Zbývá již pouze jedna hrana a vrchol c nebo d.
| a | b | c | d | e | |
| a | 2 | 2 | 2 | ||
| b | 2 | 1 | |||
| c | 2 | 1 | 2 | ||
| d | 2 | 1 | |||
| e | 2 | 1 |
| a | (0,a) | ||||
| b | (2,a) | (2,a) | |||
| c | (2,a) | (2,a) | (2,a) | (2,a) | |
| d | (∞,a) | (∞,a) | (3,e) | (3,e) | |
| e | (2,a) | (2,a) | (2,a) |
Z našeho zápisu jasně vyplývá, že vzdálenost z vrcholu a do vrcholu d je 3 a to přes vrchol e.
Z ilustrace algoritmu je souvislost Jarníkova řešení problému minimální kostry a Dijkstrova řešení nalezení nejkratších cest z daného vrcholu do ostatních již zcela patrná. V každém kroku z vrcholů ještě do modrého stromu nezařazených vybíráme v Jarníkově případě ten, který je nejblíže modrému stromu a v Dijkstrově případě ten, který je nejblíže počátečnímu vrcholu.
Pro úplnost uvádíme formulaci Dijkstrova algoritmu nalezení nejkratší cesty z daného vrcholu do ostatních vrcholů tak, jak je zapsána v práci [4]
Určení vzdálenosti z daného vrcholu nezáporně hranově ohodnoceného grafu
Vstupní data: Nezáporně hranově ohodnocený orientovaný graf G a jeho vrchol u.
Úkol: Pro každý vrchol v grafu G určit dv, vzdálenost z u do v.
Pomocné proměnné:
- M, množina vrcholů, pro které ještě není vzdálenost dv určena definitivně, pro každý vrchol v je udán vrchol Vv, který je předposledním vrcholem nejkratší cesty z u do v a neprochází vrcholy množiny M,
- Lvw, přímá vzdálenost z vrcholu v do vrcholu w.
-
[Inicializace] Je-li v = w, pak Lvw:= 0;
je-li (v,w) hrana G, pak Lvw := délka hrany (v,w);
je-li v ≠ w a (v,w) není hrana G, pak Lvw := +∞;
M := množina vrcholů G různých od u; du := 0; Vu := u;
je-li v vrchol G různý od u, položíme dv := Luv a je-li dv < +∞,
pak položíme Vv := u.
- [Test ukončení] Je-li množina M prázdná, výpočet končí.
- [Určení dv pro další vrchol] Z vrcholů množiny M vybereme vrchol v s minimální hodnotou dv (je-li jich více, pak libovolný z nich). Je-li dv = +∞, výpočet končí, jinak vyjmeme v z množiny M.
- [Aktualizace dw a Vw] Je-li v vrchol vybraný v bodě 3, pak pro každý vrchol w ležící v M provedeme v případě, že platí dv + Lvw < dw, příkazy Vw := v a dw := dv + Lvw.
- Skok do bodu 2.
Řešený příklad⇫
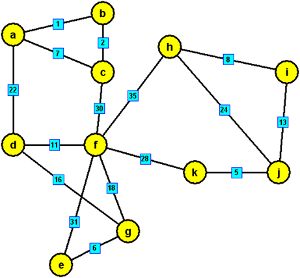
1. Určete délku nejkratších cest mezi vrcholem a a ostatními vrcholy za pomoci Dijkstrova algoritmu.
Krok 1
Začneme ve vrchole a, označíme ho modře a každému vrcholu přiradím informaci = nejkratší momentální vzdálenost od vrcholu a přes incidentní hranu s modrou kostrou (každému vrcholu, který je sousední s a, přiřadíme velikost hrany +a, vrcholu, který není incidentní, přiřadím nekonečno):
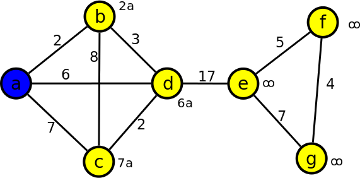
Krok 2
Projdeme hodnoty u všech vrcholů a vybereme nejmenší (u stejných se řídíme lexikografickým pravidlem).
Hodnoty: 2a, 7a, 6a, ∞, ∞, ∞. Nejmenší je 2a u vrcholu b. Do kostry vložíme vrchol b, hranu ab obarvíme modře a propočítáme hodnoty u ostatních vrcholů (u sousedů vrcholu b: když je součet hodnoty hrany a vzdáleností vrcholu b od a menší než aktuální hodnota vrcholu, tak přepíšeme aktuální hodnotu na novou +b, u vrcholu nesousedních s b, hodnota zůstává stejná):
- vrchol d – je s b spojen hranou velikosti 3, 3 + 2(vzdálenost a-b) = 5, což je menší než hodnota 6a, proto přepíšeme na 5b,
- vrchol c – je spojen s b hranou velikosti 8, 8+2 = 10, což je větší než aktuální hodnota 7a, proto necháme 7a
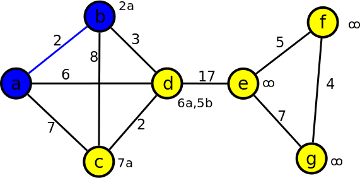
Krok 3
Hodnoty: 5b, 7a, ∞, ∞, ∞. Nejmenší je 5b u vrcholu d. Vrchol d přidáme do kostry a hranu bd obarvíme modře. Propočítáme hodnoty u ostatních vrcholů sousedních s d:
- vrchol c - je s d spojen hranou velikosti 2, 2 + 5 = 7, což je stejné jako aktuální hodnota 7a, můžeme přepsat na 7d nebo nechat 7a (osobní volna)
- vrchol e - je s d spojen hranou velikosti 17, 17 + 5 = 22, což je menší než aktuální hodnota ∞, přepíšeme na 22d
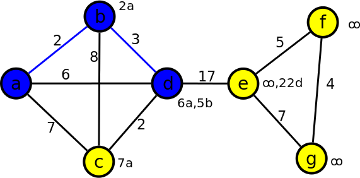
Krok 4
Hodnoty: 7a, 22d, ∞, ∞. Nejmenší hodnota je 7a u vrcholu c. Vrchol c přidáme do kostry a hranu ac obarvíme modře. Propočítáme hodnoty u ostatních vrcholů sousedních s c. Žádné vrcholy, které nepatří do kostry a jsou sousední s vrcholem c neexistují. Všechny hodnoty u ostatních vrcholů zůstanou nezměněné.
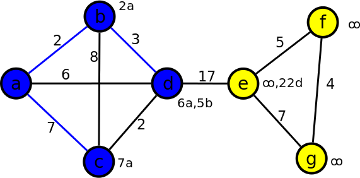
Krok 5
Hodnoty: 22d, ∞, ∞. Nejmenší je 22d u vrcholu e. Do kostry vložíme vrchol e, hranu de obarvíme modře a propočítáme hodnoty u sousedních vrcholů:
- vrchol f - je s e spojen hranou velikosti 5, 5 + 22 = 27, což je menší než nekonečno, přepíšeme na 27e
- vrchol g - je s e spojen hranou velikosti 7, 7 + 22 = 29, což je menší než ∞, přepíšeme na 29e
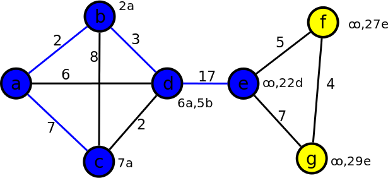
Krok 6
Hodnoty: 27e, 29e. Nejmenší je 27e u vrcholu f. Do kostry vložíme vrchol f, hranu ef obarvíme modře a propočítáme hodnoty u sousedních vrcholů:
- vrchol g - je s f spojen hranou velikosti 4, 4 + 27 = 31, což je větší než 29e, nechám aktuální hodnotu
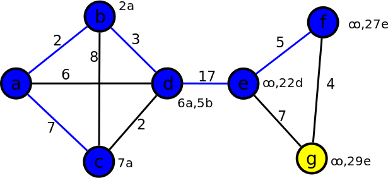
Krok 7
Hodnoty: 29e. Jediná a teda nejmenší. Vrchol g vložím do kostry a hranu eg obarvíme modře.
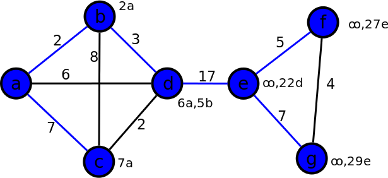
| cesta mezi vrcholy | velikost | cesta |
|---|---|---|
| a-b | 2 | a,b |
| a-c | 7 | a,c |
| a-d | 5 | a,b,d |
| a-e | 22 | a,b,d,e |
| a-f | 27 | a,b,d,e,f |
| a-g | 29 | a,b,d,e,g |
2. Najděte všechny nejkratší vzdálenosti a cesty mezi vrcholem a a ostatními vrcholy.
| a | b | c | d | e | f | g | |
| a | 2 | 7 | 6 | ||||
| b | 2 | 8 | 3 | ||||
| c | 7 | 8 | 2 | ||||
| d | 6 | 3 | 2 | 17 | |||
| e | 17 | 5 | 7 | ||||
| f | 5 | 4 | |||||
| g | 7 | 4 |
Krok 1
Začneme ve vrchole a, označíme ho modře a každému vrcholu přiradím informaci = nejkratší momentální vzdálenost od vrcholu a přes incidentní hranu s modrou kostrou (každému vrcholu, který je sousední (má v matici číslo-velikost hrany) s a, přiřadíme velikost hrany +a, vrcholu, který není incidentní (nemá v matici číslo), přiřadím nekonečno):
| a | b | c | d | e | f | g | |
| a | 2 | 7 | 6 | ||||
| b | 2 | 8 | 3 | ||||
| c | 7 | 8 | 2 | ||||
| d | 6 | 3 | 2 | 17 | |||
| e | 17 | 5 | 7 | ||||
| f | 5 | 4 | |||||
| g | 7 | 4 |
| - | |||||
| 2a | |||||
| 7a | |||||
| 6a | |||||
| ∞ | |||||
| ∞ | |||||
| ∞ |
Krok 2
Projdeme hodnoty u všech vrcholů a vybereme nejmenší (u stejných se řídíme lexikografickým pravidlem).
Hodnoty: 2a, 7a, 6a, ∞, ∞, ∞. Nejmenší je 2a u vrcholu b. Do kostry vložíme vrchol b a propočítáme hodnoty u ostatních vrcholů (u sousedů vrcholu b: když je součet hodnoty hrany a vzdáleností vrcholu b od a menší než aktuální hodnota vrcholu, tak přepíšeme aktuální hodnotu na novou +b, u vrcholu nesousedních s b, hodnota zůstává stejná):
- vrchol d – je s b spojen hranou velikosti 3, 3 + 2(vzdálenost a-b) = 5, což je menší než hodnota 6a, proto přepíšeme na 5b,
- vrchol c – je spojen s b hranou velikosti 8, 8+2 = 10, což je větší než aktuální hodnota 7a, proto necháme 7a
| a | b | c | d | e | f | g | |
| a | 2 | 7 | 6 | ||||
| b | 2 | 8 | 3 | ||||
| c | 7 | 8 | 2 | ||||
| d | 6 | 3 | 2 | 17 | |||
| e | 17 | 5 | 7 | ||||
| f | 5 | 4 | |||||
| g | 7 | 4 |
| - | - | ||||
| 2a | - | ||||
| 7a | 7a | ||||
| 6a | 5b | ||||
| ∞ | ∞ | ||||
| ∞ | ∞ | ||||
| ∞ | ∞ |
Krok 3
Hodnoty: 7a, 5b, ∞, ∞, ∞. Nejmenší je 5b u vrcholu d. Vrchol d přidáme do kostry. Propočítáme hodnoty u ostatních vrcholů sousedních s d:
- vrchol c - je s d spojen hranou velikosti 2, 2 + 5 = 7, což je stejná jako aktuální hodnota 7a, můžeme přepsat na 7d nebo nechat 7a (osobní volba)
- vrchol e - je s d spojen hranou velikosti 17, 17 + 5 = 22, což je menší než aktuální hodnota ∞, přepíšeme na 22d
| a | b | c | d | e | f | g | |
| a | 2 | 7 | 6 | ||||
| b | 2 | 8 | 3 | ||||
| c | 7 | 8 | 2 | ||||
| d | 6 | 3 | 2 | 17 | |||
| e | 17 | 5 | 7 | ||||
| f | 5 | 4 | |||||
| g | 7 | 4 |
| - | - | - | |||
| 2a | - | - | |||
| 7a | 7a | 7a | |||
| 6a | 5b | - | |||
| ∞ | ∞ | 22d | |||
| ∞ | ∞ | ∞ | |||
| ∞ | ∞ | ∞ |
Krok 4
Hodnoty: 7a, 22d, ∞, ∞. Nejmenší hodnota je 7a u vrcholu c. Vrchol c přidáme do kostry. Propočítáme hodnoty u ostatních vrcholů sousedních s c. Žádné vrcholy, které nepatří do kostry a jsou sousední s vrcholem c neexistují. Všechny hodnoty u ostatních vrcholů zůstanou nezměněné.
| a | b | c | d | e | f | g | |
| a | 2 | 7 | 6 | ||||
| b | 2 | 8 | 3 | ||||
| c | 7 | 8 | 2 | ||||
| d | 6 | 3 | 2 | 17 | |||
| e | 17 | 5 | 7 | ||||
| f | 5 | 4 | |||||
| g | 7 | 4 |
| - | - | - | - | ||
| 2a | - | - | - | ||
| 7a | 7a | 7a | - | ||
| 6a | 5b | - | - | ||
| ∞ | ∞ | 22d | 22d | ||
| ∞ | ∞ | ∞ | ∞ | ||
| ∞ | ∞ | ∞ | ∞ |
Krok 5
Hodnoty: 22d, ∞, ∞. Nejmenší je 22d u vrcholu e. Do kostry vložíme vrchol e a propočítáme hodnoty u sousedních vrcholů:
- vrchol f - je s e spojen hranou velikosti 5, 5 + 22 = 27, což je menší než nekonečno, přepíšeme na 27e
- vrchol g - je s e spojen hranou velikosti 7, 7 + 22 = 29, což je menší než ∞, přepíšeme na 29e
| a | b | c | d | e | f | g | |
| a | 2 | 7 | 6 | ||||
| b | 2 | 8 | 3 | ||||
| c | 7 | 8 | 2 | ||||
| d | 6 | 3 | 2 | 17 | |||
| e | 17 | 5 | 7 | ||||
| f | 5 | 4 | |||||
| g | 7 | 4 |
| - | - | - | - | - | |
| 2a | - | - | - | - | |
| 7a | 7a | 7a | - | - | |
| 6a | 5b | - | - | - | |
| ∞ | ∞ | 22d | 22d | - | |
| ∞ | ∞ | ∞ | ∞ | 27e | |
| ∞ | ∞ | ∞ | ∞ | 29e |
Krok 6
Hodnoty: 27e, 29e. Nejmenší je 27e u vrcholu f. Do kostry vložíme vrchol f a propočítáme hodnoty u sousedních vrcholů:
- vrchol g - je s f spojen hranou velikosti 4, 4 + 27 = 31, což je větší než 29e, nechám aktuální hodnotu
| a | b | c | d | e | f | g | |
| a | 2 | 7 | 6 | ||||
| b | 2 | 8 | 3 | ||||
| c | 7 | 8 | 2 | ||||
| d | 6 | 3 | 2 | 17 | |||
| e | 17 | 5 | 7 | ||||
| f | 5 | 4 | |||||
| g | 7 | 4 |
| - | - | - | - | - | - |
| 2a | - | - | - | - | - |
| 7a | 7a | 7a | - | - | - |
| 6a | 5b | - | - | - | - |
| ∞ | ∞ | 22d | 22d | - | - |
| ∞ | ∞ | ∞ | ∞ | 27e | - |
| ∞ | ∞ | ∞ | ∞ | 29e | 29e |
Krok 7
Hodnoty: 29e. Jediná a teda nejmenší. Vrchol g vložím do kostry.
| a | b | c | d | e | f | g | |
| a | 2 | 7 | 6 | ||||
| b | 2 | 8 | 3 | ||||
| c | 7 | 8 | 2 | ||||
| d | 6 | 3 | 2 | 17 | |||
| e | 17 | 5 | 7 | ||||
| f | 5 | 4 | |||||
| g | 7 | 4 |
| - | - | - | - | - | - |
| 2a | - | - | - | - | - |
| 7a | 7a | 7a | - | - | - |
| 6a | 5b | - | - | - | - |
| ∞ | ∞ | 22d | 22d | - | - |
| ∞ | ∞ | ∞ | ∞ | 27e | - |
| ∞ | ∞ | ∞ | ∞ | 29e | 29e |
Krok 8
Úlohy k řešení ⇫
1. Kolik nejvíce vrcholů může mít graf, který má největší možnou vzdálenost mezi dvěma vrcholy rovnou 2?
Výsledek
počet vrcholů není omezen
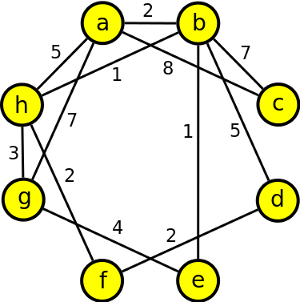
2. Jaké jsou vzdálenosti všech vrcholů od vrcholu a?
Výsledek
dG(a,a) = 0, dG(a,b) = 2, dG(a,c) = 8, dG(a,d) = 7, dG(a,e) = 3, dG(a,f) = 5, dG(a,g) = 6, dG(a,h) = 3
3. V jakém pořadí budou zpracovány vrcholy při běhu Dijkstrova algoritmu s výchozím vrcholem a?
Výsledek
a, b, h, e, f, g, d, c nebo a, b, e, h, f, g, d, c
4. Dijkstrovým algoritmem určete vzdálenost a minimální cestu všech vrcholů od vrcholu a.
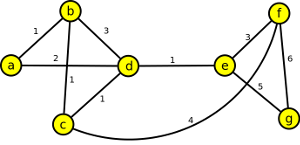
Výsledek
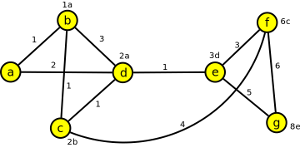
| Vrchol | Vzdálenost od a | Min. cesta od a | |
| b | - | 1 | ab |
| c | - | 2 | abc |
| d | - | 2 | ad |
| e | - | 3 | ade |
| f | - | 6 | abcf |
| g | - | 8 | adeg |
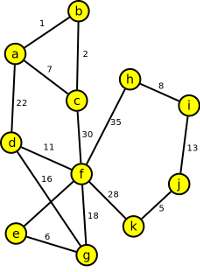
5. Určete vzdálenost vrcholu j od vrcholu a.
Zdroje textů
- DIMA - diskrétní matematika, http://oliva.uhk.cz
- Dijkstrův algoritmus, http://www.algoritmy.net/article/5108/Dijkstruv-algoritmus
- Kovář, Petr. DISKRÉTNÍ MATEMATIKA a ÚVOD DO TEORIE GRAFŮ ( příklady k procvičení ), 2012
- Kučera, L.. Kombinatorické algoritmy. Praha: SNTL, 1989