Bipartitní grafy

Obsah ⇫

bipartitní graf
příklady bipartitních grafů
jak zjistit, zda je graf bipartitní (nutná a postačující podmínka bipartitního grafu)

Graf G=(V,E) nazveme bipartitní, jestliže vrcholy množiny V můžeme rozdělit do dvou vrcholově disjunktních množin V1 a V2 tak, že každá hrana grafu G má jeden koncový vrchol v množině V1 a druhý v množině V2.

Příklady bipartitních grafů:

Graf G1 je bipartitní graf, kterého vrcholová množina se dá rozdělit do množin V1 a V2 a hrany se vyskytují jenom mezi vrcholy z různých množin. Izolovaný vrchol můžeme přidělit jak do množiny V1, tak do množiny V2. Graf G2 je kompletní bipartitní graf K3,1. Graf G3 je kompletní bipartitní graf K3,3.

Příklad

Do tanečních chodí čtyři chlapci - Petr, Adam, Jirka, Roman a čtyři dívky - Jana, Pavla, Zdena a Bára. Je možné vytvořit traneční páry, které se vzájemně znají, jestliže Petr zná Janu a Zdenu, Adam zná Janu a Pavlu, Bára zná Romana a Jirku a Jirka zná Janu a Báru?

Nakreslíme si bipartitní graf, kde jednu množinu vrcholů budou tvořit chlapci a druhou množinu dívky. Hrany pak budou tvořit vzájemné známosti.

P -	Petr	J -	Jana
A -	Adam	P -	Pavla
J -	Jirka	Z -	Zdena
R -	Roman	B -	Bára

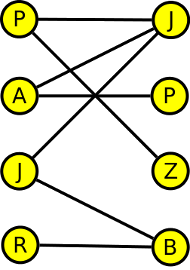
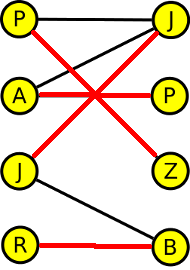
Z grafu už jasně vidíme, že Roman má jedinou možnost vytvořit pár s Bárou. Tím už nemůžeme použít hranu JB a tak Jirka může tvořit pár pouze s Janou. Potom už nemůžeme použít ani hrany PJ a AJ a tak Adam může tvořit pár pouze s Pavlou a Petr se Zdenou. Páry tak budou tvořit: Roman a Bára, Jirka a Jana, Adam a Pavla a Petr a Zdena.

Jak zjistit, zda graf je bipartitní?

Zjišťování, zda se vrcholy grafu dají rozdělit do dvou disjunktních množin tak, aby se hrana vyskytovala pouze mezi vrcholy z různých množin, není jednoduché zvláště u větších grafů.Proto nás zajímá, zda neexistuje i jiný způsob, jak zjistit, zda graf je či není bipartitní. Na to nám odpoví následující věta:

Věta:: ∀G=(V,E): Graf G je bipartitní právě tehdy, když neobsahuje kružnici liché délky.

Než provedeme důkaz věty, dokážeme následující dvě lemmy:

Lemma:: Každý uzavřený sled liché délky obsahuje jako podgraf kružnici.

Důkaz sporem:: Nechť tvrzení neplatí, pak: Existuje uzavřený sled liché délky, který neobsahuje jako podgraf kružnici. Nechť S je uzavřený sled v grafu G, který neobsahuje jako podgraf kružnici a nechť S´ je indukovaný podgraf grafu G na všech vrcholech sledu S. Protože S neobsahuje kružnici ⇒ S´ je strom a protože S je uzavřený sled (musíme se vrátit do výchozího vrcholu), pak pro každou hranu S´ platí: tolik krát, kolikrát půjdeme po hraně tam (jedním směrem →), musíme jít po téže hraně i zpět (opačným směrem ←) ⇒ po každé hraně S´ projdeme sudý počet krát a to je spor s tím, že S je uzavřený sled liché délky.∎

Lemma:: Uzavřený sled liché délky obsahuje kružnici liché délky.

Důkaz provedeme indukcí dle délky uzavřeného sledu:

Nejkratší uzavřený sled je délky tři. Tento sled je zřejmě kružnice liché délky.
Nechť lemma platí pro uzavřený sled délky k, k≥3, k je liché číslo - indukční předpoklad. Dokážeme je i pro sled S=(v0,e1,v1,...,ek+2,v0) liché délky (k + 2). Pro sled S mohou nastat dva případy:
1. Sled S je kružnice. Pak je lemma dokázána.
2. Sled S není kružnice. Pak ale zřejmě musí alespoň jednu kružnici C=(vi,ei+1,vi+1,...,ej,vj=vi) obsahovat (podle předchozí lemmy). Je-li kružnice C liché délky, opět jsme s důkazem hotovi. Je-li sudé délky, pak S-(vi,ei+1,vi+1,...,ej) je uzavřený sled liché délky, a to délky menší než k. Podle indukčního předpokladu, pak v S-(vi,ei+1,vi+1,...,ej) existuje kružnice liché délky.∎

Věta:: Graf je bipartitní právě tehdy, když neobsahuje kružnici liché délky.

Důkaz:

⇒ nepřímo, tj.:

Jestliže G obsahuje kružnici liché délky, pak G není bipartitní.

G obsahuje kružnici liché délky, např. C=(x1,x2,...,x2k+1). Zkusme vrcholy kružnice rozdělit do dvou množin tak, aby hrany byly jenom mezi vrcholy z různých množin. Vrchol x1 dáme do množiny V1, pak vrchol x2 musíme dát do V2, protože existuje hrana {x1,x2} a takhle budeme pokračovat dál..., x2l-1 do Vl(l=2,...,k+1), x2s do V2(s=2,...,k). Vidíme, že vrchol x2(k+1)-1=x2k+1 bude v množině V1, jenomže ve V1 se nachází také x1 a existuje hrana {x1,x2k+1}. Vrcholy kružnice liché délky se nedají rozdělit do dvou množin tak, abych existovala hrana jenom mezi vrcholy z různých množin. A když se vrcholy tak rozdělit nedají, pak podle definice bipartitního grafu, to není bipartitní graf.

⇐dokážeme sporem. Předpokládejme pro spor, že existuje graf G neobsahující kružnici liché délky a zároveň graf G není bipartitní. Bez újmy na obecnosti můžeme předpokládat, že graf G je souvislý. Zvolme pevně vrchol v v grafu G a definujme množiny V1 a V2 takto:

v'∈V1, jestliže délka nejkratší cesty z v do v' je sudé číslo,
v''∈V2, jestliže délka nejkratší cesty z v do v'' je liché číslo.

Protože graf G není bipartitní, existuje v něm alespoň jedna hrana e={x,y} s oběma koncovými vrcholy ležícími v téže množině, např. v množině V1 (pro V2 proběhne důkaz analogicky). Pak ale nejkratší cesta z vrcholu x do vrcholu v spolu s nejkratší cestou z vrcholu v do vrcholu y je sledem sudé délky a spolu s hranou e tvoří uzavřený sled liché délky v grafu G. Tento sled však dle předchozího lemma obsahuje kružnici liché délky. Ale to je spor s předpokladem.∎

Řešený příklad ⇫

1. Existuje bipartitní graf se skóre (3,3,3,5,6,6,6,6,6,6,6)?

Krok 1

Každý bipartitní graf má vrcholy rozděleny do dvou skupin - V1 a V2. Součty stupňů obou skupin si musí být rovny.

Krok 2

Z uvedených čísel je zřejmé, že jejich součet je 56. Každá ze skupin vrcholů musí tedy mít součet skóre 28.

Krok 3

Z uvedených čísel není možné poskládat dvě skupiny se součtem 28. To je sudé číslo. Ve skóre grafu máme čtyři lichá čísla, proto by v každé skupině vrcholů musela být dvě nebo čtyři tato čísla. Pokud by byla rozdělena po dvou v každé skupině, skóre by se lišilo o 2. Ze zbylých sedmi šestek ale dvě skupiny lišící se o 2 nevytvoříme. Pokud by byla všecha čtyři v jedné skupině, jejich součet je 14, což není násobek šesti a skóre skupin by se nám pak také nerovnala, neboť v druhé skupině by byly pouze vrcholy stupně 6. Nejedná se tudíž o skóre bipartitního grafu.

2. Určete počet všech úplných bipartitních podgrafů K1,3 úplného bipartitního grafu K3,3.

Krok 1

Uvědomme si, že množinu tří vrcholů můžeme vybírat z tří vrcholů obou množin K3,3 a množinu jednoho vrcholu také z obou mnoižin K3,3.

Krok 2

Výsledný počet grafů tak bude $(\begin{matrix} 3 \\ 1 \end{matrix}) \cdot (\begin{matrix} 3 \\ 3 \end{matrix}) + (\begin{matrix} 3 \\ 3 \end{matrix}) \cdot (\begin{matrix} 3 \\ 1 \end{matrix})$ .

3. Představte si, že hodláte k sobě domů na večeři pozvat 8 kamarádů (označme je a,b,c,d,e,f,g,h). Někteří z nich se již znají. Večeři budete podávat u dvou stolů. Zjistěte, zda by bylo možné posadit své kamarády ke dvěma stolům tak, aby u každého stolu seděli jen ti, kteří se navzájem neznají (aby mohli rozšířit okruh svých známých). Níže je uveden přehled vašich kamarádů, kteří se již znají:

a	-	d,	f,	g
b	-	c,	d,	h
c	-	b,	e
d	-	a,	b,	f
e	-	c,	f
f	-	a,	d,	e
g	-	a
h	-	b

Krok 1

Jedno z možných řešení je následujíci:

Nakreslíme si graf podle zadaného seznamu sousedních vrcholů a to tak, že vrcholy budou jednotliví kamarádi a hrany budou reprezentovat jejich vzájemnou známost.

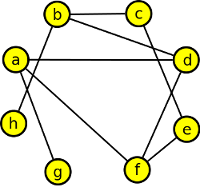
Krok 2

Z grafu již lehce zjistíme, zda je to graf birartitní. Bipartitní graf určujeme proto, že osoby v každé ze dvou množin grafu se vzájemně neznaji - nevede mezi nimi hrana. A jak vidíme, v grafu se nachází kružnice liché délky (a,d,f), proto můžeme prohlásit, že není možné posadit kamarády ke dvěma stolům tak, aby se vzájemně neznali.

Úlohy k řešení ⇫

1. Jsou následující grafy bipartitní?

Výsledek

a - ne, obsahuje kružnice liché délky, b - ano, c - ano, d - ne, obsahuje kružnici liché délky, e - ne, obsahuje kružnici liché délky

2. Kolik existuje různých bipartitních grafů na m + n vrcholech. Rozlišujeme pojmenování vrcholů?

Výsledek

2mn

3. Pro jaké hodnoty m,n > 0 je úplný bipartitní graf Km,n zároveň kružnicí?

Výsledek

Pro m = n = 2, délky čtyři.

4. Jaká je největší vzdálenost dvou vrcholů v úplném bipartitním grafu K33,44 ? (představte si, jak kompletní bipartitní graf vypadá)

Výsledek

Konkurz

5. Jedna instituce vypsala konkurz na obsazení 5 míst pro překladatele, a to z ruštiny, němčiny, angličtiny, francouzštiny a španělštiny. Přihlásilo se 5 uchazečů, kteří ovládali některé z těchto jazyků. Bárta ovládal všech 5 jazyků, Kopal angličtinu, francouzštinu a ruštinu, Lehký němčinu a ruštinu, Novák angličtinu a němčinu a Zeman ruštinu a němčinu. Mohla instituce přijetím těchto uchazečů obsadit místa tak, aby každý z nich předkládal jen z jednoho jazyka? Pokud ano, navrhněte řešení.

Výsledek

španělština - Bárta, francouzština - Kopal, anglinčtina - Novák, němčina - Zeman, ruština - Lehký

6. Napište matici sousednosti grafu K2,3.

Výsledek

0	0	1	1	1
0	0	1	1	1
1	1	0	0	0
1	1	0	0	0
1	1	0	0	0

7. Kolik hran má úplný bipartitní graf K4,5?

Výsledek

4∙5 = 20 hran

8. Určete počet všech úplných bipartitních podgrafů K1,3 úplného bipartitního grafu K2,3.

Výsledek

$(\begin{matrix} 2 \\ 1 \end{matrix}) \cdot (\begin{matrix} 3 \\ 3 \end{matrix})$ - množinu tří vrcholů vybíráme z množiny tří a množinu jednoho vrcholu z množiny dvou. Jinak to nejde.

9. Dokažte, že Kn má n(n-1)/2 hran. Kolik hran má graf Kr,s? Dokažte to!

Výsledek

Důkaz přímo:

Pro každý graf, teda i pro Kn platí věta o sudosti:

$\sum_{i = 1}^{n} deg(v_{i}) = 2 m$ ⇒ deg(v1)+deg(v2)+...+deg(vn)=2m

V kompletním grafu s n vrcholy platí: ∀vi, i=1,...,n: deg(vi)=n-1

z toho všeho plyne:

$\underset{n - krát}{\underset{⏟}{n - 1 + n - 1 + ... n - 1}} = 2m$ ⇒ n(n-1) = 2m ⇒ m= n(n-1)/2,

Kr,s je úplný bipartitní graf, kterého množina vrcholů se dá rozdělit do dvou disjunktních množin V1,V2, přičemž hrany jsou jenom mezi vrcholy vi,vj , přičemž vi∈V1, vj∈V2, i=1,...,r, j=r+1,...,s,|V1|=r, |V2|=s . Protože Kr,s je úplný bipartitní graf, tak každý vrchol z V1 množiny sousedí s každým vrcholem z množiny V2 a naopak každý vrchol z V2 množiny sousedí s každým vrcholem z množiny V1 ⇒ ∀vi∈V1 i=1,...,r: deg(vi)=s a ∀ vj∈V2 i=r+1,...,n: deg(vj)=r ⇒

⇒ $\underset{vrcholy z V_{1}}{\underset{⏟}{\deg (v_{1}) + \deg (v_{2}) + ... + \deg (v_{r})}} + \underset{vrcholy z V_{2}}{\underset{⏟}{\deg (v_{r + 1}) + ... + \deg (v_{n})}} = 2m$ ⇒

⇒ $\underset{r - krát}{\underset{⏟}{s + s + ... + s}} + \underset{s - krát}{\underset{⏟}{r + r + ... + r}} = 2m$ ⇒ r∙s+s∙r = 2m ⇒ 2rs = 2m ⇒ m = rs.

Zdroje textů

DIMA - diskrétní matematika, http://oliva.uhk.cz
Hliněný, Petr. Diskrétní Matematika (456-533 DIM), 2006
Kovář, Petr. DISKRÉTNÍ MATEMATIKA a ÚVOD DO TEORIE GRAFŮ ( příklady k procvičení ), 2012

DIMA - Teorie grafů

Bipartitní grafy

Obsah ⇫

Teorie ⇫

Definice bipartitního grafu:

Řešený příklad ⇫

Úlohy k řešení ⇫

Zdroje textů