Základní terminologie

Obsah ⇫

definice grafu, nakreslení grafu
koncové vrcholy grafu, incidentnost a sousednost vrcholů
podgraf – faktorový, indukovaný
stupeň vrcholu
multigraf, pseudograf
kompletní (úplný) graf, bipartitní graf a regulární graf
odebrání vrcholu / hrany
sled, tah, cesta, kružnice
souvislost vrcholů, souvislý graf
komponenta grafu
artikulace a most v grafu
vzdálenost dvou vrcholů v grafu
izomorfismus dvou grafů
matice sousednosti grafu
seznam sousedních vrcholů
incidenční matice grafu
doplněk/komplement grafu
skóre grafu (grafová posloupnost)

Pod pojmem obyčejný graf G rozumíme uspořádanou dvojicí (V,E) (G = (V,E)), kde V je libovolná množina a E⊆P2(V) (P2(V) = všechny dvouprvkové podmnožiny množiny V, prvek množiny E je dvouprvková podmnožina množiny V). Když jsou množiny V,E konečné, nazýváme graf G konečným, když jsou V,E nekonečné, tak G je nekonečný. Prvky množiny V budeme nazývat vrcholy, prvky E hrany grafu G. Každá hrana grafu G je určená dvěma vrcholy, zapisujeme e={vi,vj}, zkráceně vivj, vi,vj∈V,e∈E. Počet prvků množiny V značíme |V| nebo n a počet prvků množiny E značíme |E| nebo m (v některé literatuře se můžete setkat s označením |V|=p, |E|=q).

Pozn.: Označení množiny vrcholů V a množiny hran E vychází z anglických termínů vertex a edge.

V celém textu, pokud nebude uvedeno jinak, pod pojmem graf máme na mysli obyčejný graf.

Pod nakreslením grafu G rozumíme reprezentaci grafu G, v kterém prvky množiny V jsou reprezentované body a prvky množiny E jsou reprezentované oblouky/rovnými čárami (koncové body oblouku/rovné čáry jsou totožné s body vrcholů, které tvoří hranu odpovídajícího oblouku).


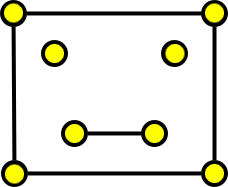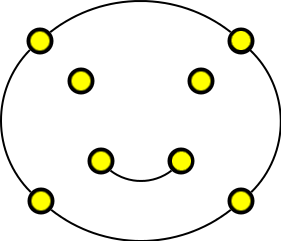Obrázek 1: příklad grafu	Obrázek 2: jiný příklad grafu

Příklad

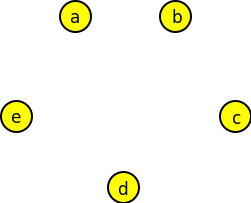
Nakreslete graf G(V,E), je-li dáno V={a,b,c,d,e} a E={ab,ac,ad,ae}.


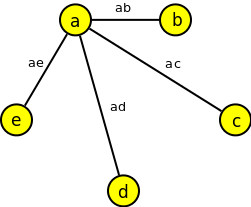Nejprve nakreslíme vrcholy V,	potom je doplníme o hrany E.

Definice - koncové vrcholy, incidentnost, sousednost:

Nechť e = {v,w} je hrana grafu G. Vrcholy v,w nazýváme koncovými vrcholy hrany e nebo též vrchol v (vrchol w) a hrana e jsou incidentní. O koncových vrcholech v a w hrany e budeme říkat, že jsou sousední, podobně hrany ek a el jsou sousední, když incidují se společným vrcholem.

incidentnost

v,w – sousední vrcholy, ek,el – sousední hrany, e inciduje s v, e inciduje s w, ek inciduje s u, el inciduje s u

Definice podgrafu – faktorový, indukovaný:

Podgrafem grafu G = (V,E) budeme nazývat graf G´ = (V´,E´,) pro který V´⊆V,E´⊆E, přičemž e´ = (v,w)∈E´ jenom když v,w∈V´; označujeme G´⊆G.

Graf G = (V,E) se rovná grafu G' = (V',E'), jestliže V = V' a E = E'.

Když V´ = V, pak graf G´ se nazývá faktorový podgraf grafu G nebo faktor grafu G.

Nechť V´⊆V (V´ je podmnožina V) grafu G = (V,E). Pak podgraf G´ = (V´,E´) je indukovaný podgraf grafu G, indukovaný množinou vrcholů V´, když G´ obsahuje všechny hrany spojující vrcholy z V´ v grafu G. Podgraf G´ indukovaný množinou vrcholů V´ v grafu G budeme označovat <V´>G.

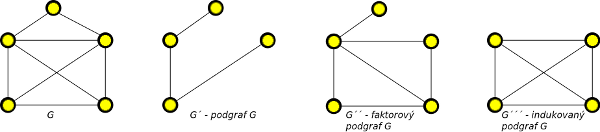
podgrafy

Graf spolu s ukázkou podgrafu, faktorového podgrafu a indukovaného podgrafu

Příklad

Je graf G´ faktorový nebo indukovaný podgraf grafu G?

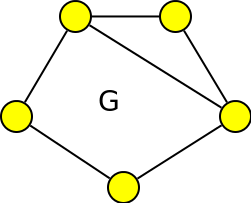
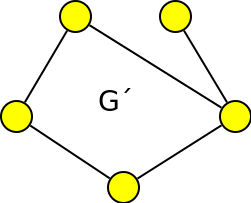
grag G podgraf G´

Nejprve zkontrolujeme, jedná-li se skutečně o podgraf, tj. zda V´⊆V a E´⊆E.

Jelikož je to podgraf, zkontrolujeme, zda V = V´, tj. zda mají oba grafy stejný počet vrcholů.

Jelikož V = V´, jedná se o faktorový podgraf.

Definice stupně vrcholu:

Počet hran incidentních s vrcholem v v grafu G nazýváme stupeň vrcholu v a označujeme ho degGv nebo stručně deg v nebo dG(v). Symboly δ(G) a Δ(G) označujeme nejmenší a největší ze stupňů vrcholů grafu G. Vrchol, který má stupeň 0 nazýváme izolovaný vrchol. Vrchol stupně 1 se nazývá visící vrchol.

Označení degG(v) vychází z anglického termínu degree.

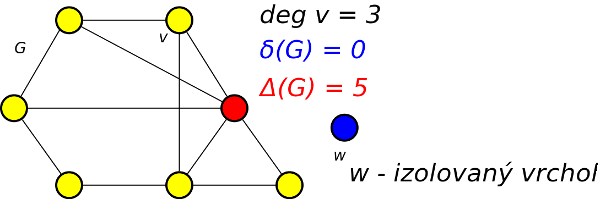
stupně vrcholu

V grafu je vrchol v stupně 3, minimální stupeň grafu je 0, nejvyšší stupeň je 5.

Příklad

Jaký je největší a nejmenší stupeň vrcholu v grafu K5?

Graf označený jako K5 je graf, který má pět vrcholů a všechny vrcholy jsou mezi sebou propojeny hranami. Z každého vrcholu tak vedou čtyři hrany k zbývajícím vrcholům a proto má každý vrchol stupeň čtyři. Proto nejmenší i největší stupeň grafu je čtyři.

Definice – multigraf, pseudograf:

Multigrafem GM = (VM,EM) budeme nazývat graf, kterého prvky množiny EM nazýváme multihrany. Každá multihrana je určená dvěma vrcholy a několika žebry (jednoduchými hranami), které jsou incidentní s těmito dvěma vrcholy.

Když dovolíme, aby hrana e byla určená jenom jedním vrcholem v (tj. aby koncové vrcholy hrany e byly totožné), tak hranu e nazýváme smyčkou. Když v definici multigrafu dovolíme i smyčky, tak daný graf bude pseudograf.

Grafy, které nejsou multigrafy, budeme nazývat obyčejné grafy.

multigraf

Definice kompletního (úplného) grafu

Kompletní graf je graf, ve kterém každá dvojice vrcholů je sousední. Kompletní graf s n vrcholy označujeme Kn.

Graf Kn má n(n-1)/2 hran.

Definice bipartitního grafu

Graf G je bipartitní, když jeho vrcholová množina V může být rozdělená do dvou podmnožin V1 a V2 tak, že každá hrana z E má jeden koncový vrchol ve V1 a druhý ve V2, označujeme G = (V1,V2;E). Když v grafu G = (V1,V2;E) je každý vrchol v z V1 spojený s každým vrcholem w z V2, tak graf G se nazývá kompletní bipartitní graf, označujeme Kr,s,|V1| = r, V2 = s.

Graf Kr,s má r∙s hran.

Definice regulárního grafu

Graf G je regulární (pravidelný), když všechny vrcholy grafu G jsou stejného stupně. Když graf G je regulární s degvi = r pro všechny vrcholy vi∈V(G), pak G se jmenuje r-regulární (Kn je n-1 regulární).

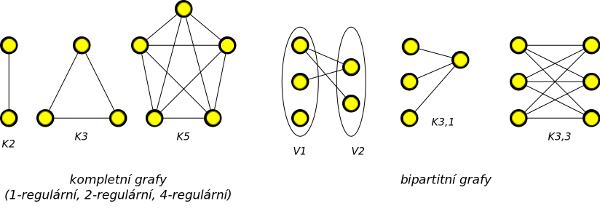
kompletní a bipartitní grafy

příklad kompletního, bipartitního a regulárních grafů

Příklad

Srovnejme grafy K10,10 a K19 .

Který má více vrcholů?
Který má více hran?

Graf K10,10 má 10 + 10 = 20 vrcholů, graf K19 má vrcholů 19.

Graf K10,10 má 10 ∙ 10 = 100 hran, graf K19 má hran 19 ∙ 18 / 2 = 171.

Definice odebrání vrcholu

Nechť je dán graf G = (V,E), v∈V a e∈E. Graf G - v značí graf, který dostaneme z grafu G odebráním vrcholu v a všech hran s vrcholem v incidentních, tj. G - v = (V - {v}, {e∈E; v není incidentní s e}).

Definice odebrání hrany

Graf G – e značí graf získaný z grafu G odebráním hrany e, tj. G - e = (V,E – {e}).

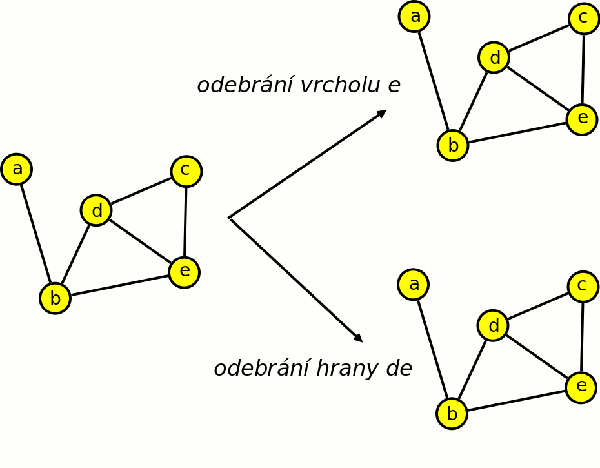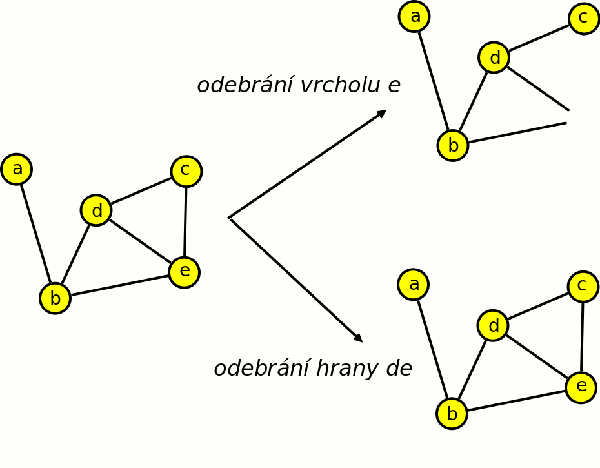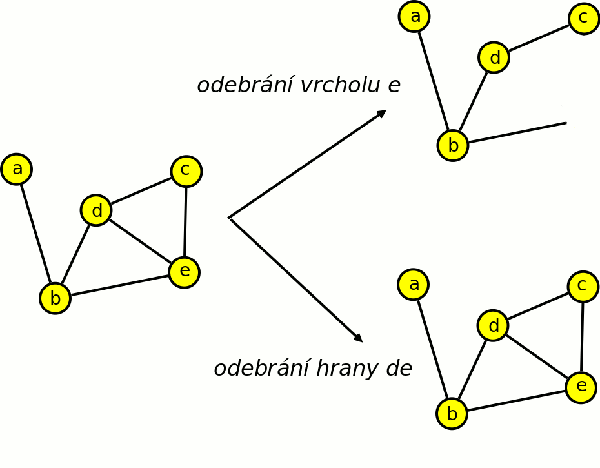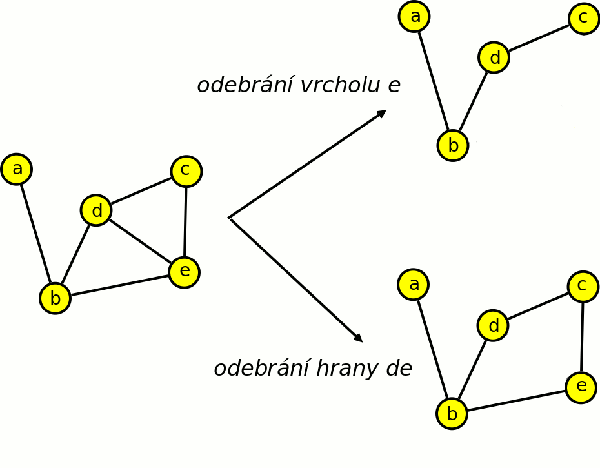
odebrání vrcholu

Pro každý graf platí následující tvrzení:

Věta (princip sudosti):

Když obyčejný graf G má m hran, tak součet stupňů všech jeho vrcholů se rovná 2m:

$\sum_{v \in V} \deg_{G} v = 2 m$

Důkaz 1 (matematickou indukcí vzhledem k počtu hran m):

Když m = 0, pak se stupně všech vrcholů grafů rovnají 0 (všechny vrcholy jsou izolované), tedy věta pro m = 0 platí.
Předpokládejme, že věta platí pro všechny grafy s méně než m hranami a nechť G je graf, který má právě m hran. Nechť e je hrana grafu G. Bez ujmy na všeobecnost můžeme předpokládat, že vrcholy grafu jsou označeny v1,v2,...,vn a e = v1,v2.

Po vynechání hrany e z grafu G dostaneme graf H = G-e, který má n vrcholů a m-1 hrán. Pro stupně vrcholů platí: degHv1 = degGv1-1, degHv2=degGv2-1, degHvi = degGvi, i = 3,...,n.

Podle indukčního předpokladu pro součet stupňů vrcholů grafu H platí:

$\sum_{v \in V (H)} \deg_{H} v = 2 (m - 1)$ .

Počítejme teď součet stupňů pro graf G:

$\sum_{i = 1}^{n} \deg_{G} v_{i} = \deg_{H} v_{1} + 1 + \deg_{H} v_{2} + 1 + \deg_{H} v_{3} + ... + \deg_{H} v_{n}$

$\sum_{i = 1}^{n} \deg_{H} v_{i} + 2 = 2 (m - 1) + 2 = 2m - 2 + 2 = 2m$ ⇒ věta platí pro všechny grafy.∎

Důkaz 2:

Každá hrana grafu G je incidentní s dvěma vrcholy, každý vrchol vi je incidentní s pi hranami, kde pi = degG(vi), i = 1,...,n.

Označme M množinu všech uspořádaných dvojic (v,e), kde v je vrchol incidentní s hranou e, tj. M = {(v,e);v∈e}.

Na tuto množinu se podívejme jednak z pohledu jednotlivých vrcholů daného grafu G a jednak z pohledu hran grafu G.

Označme Mv = {(v,e);v∈e}∀v∈V a Me = {(v,e);v∈e}∀e∈E.

Je zřejmé, že platí následující vztahy:

|Mv| = degG(v) ∀v∈V,
|Me| = 2 ∀e∈E,
$\underset{v \in V}{∐} M_{v} = M = \underset{e \in E}{∐} M_{e}$ ,
Mv∩Mv´ = Ø ∀v≠v´,
Me∩Me´ = Ø ∀e≠e´.

Odtud $∣ \underset{v \in V}{∐} M_{v} ∣ = \sum_{v \in V} ∣ M_{v} ∣ = ∣ M ∣ = ∣ \underset{e \in E}{∐} M_{e} ∣ = \sum_{e \in E} ∣ M_{e} ∣ = \sum_{e \in E} 2 = ∣ E ∣ \cdot 2 = 2 \cdot ∣ E ∣$ .∎

Příklad

Nechť graf má n vrcholů, čtyři vrcholy stupně 5 a ostatní vrcholy stupně 4 a počet hran se rovná 44. Kolik má graf vrcholů (tj. čemu se rovná n)?

K vyřešení zadání použijeme Větu o principu sudosti: Součet stupňů všech vrcholů n je dvakrát větší, než je počet hran m.

Známe:

4 vrcholy stupně 5
(n-4) vrcholů stupně 4
počet hran m=44

5+5+5+5+4+4.....+4=2∙m 4+4.....+4 → (n-4) vrcholů stupně 4

Tuto úvahu přepíšeme do rovnice: 5∙4+(n-4)∙4=2∙44 a vyřešíme.

20+4n-16=88

4n+4=88

4n=84

n=21

Můžeme tedy prohlásit, že počet vrcholů grafu je 21.

Důsledek:: Počet vrcholů lichého stupně v grafu je sudý.

Příklad

Sedm přátel se rozhodlo, že si budou přes prázdniny dopisovat. Dohodli se, že každý bude udržovat styk právě se třemi přáteli. Nepodařilo se jim to. Proč?

Když si danou úlohu přetransformujeme do grafu: vrcholy budou přátelé a dva vrcholy spojíme, když si dopisují, tak by měl vzniknout 3-regulární graf na 7 vrcholech. A takový graf neexistuje, neboť počet vrcholů lichého stupně je v každém grafu sudý.

Definice sledu:

Sled v grafu G je konečná posloupnost S = (v0,e1,v1,e2,...,vk-1,ek,vk), v které se střídají vrcholy a hrany, a která začíná a končí ve vrcholu, přičemž pro všechna i = 1,...,k je ei = (vi-1,vi); hovoříme také o v0-vk sledu. Vrchol v0 nazýváme začátkem, vrchol vk koncem sledu S, ostatní vrcholy se nazývají vnitřní vrcholy sledu S. Ve sledu se hrany a vrcholy můžou opakovat. Číslo k nazveme délkou sledu S. Sled nazýváme uzavřený, když jeho začátek a konec jsou totožné. V opačném případě ho nazýváme otevřený.

Sled je vlastně jakási procházka po grafu, při které můžeme libovolný vrchol navštívit vícekrát, můžeme dokonce i projít vícekrát po téže hraně.

Definice tahu:

Tah je takový sled, ve kterém se žádná hrana nevyskytuje dvakrát. Tah nazýváme uzavřený, když jeho začátek a konec jsou totožné. V opačném případě ho nazýváme otevřený.

Definice cesty:

Otevřený tah, ve kterém jsou všechny vrcholy navzájem různé, se nazývá cesta. Počet hran v cestě se nazývá délka cesty.

Definice kružnice:

Uzavřená cesta se nazývá kružnice. Délka kružnice je počet hran/vrcholů (počet hran a vrcholů je stejný).

Orientované kružnici se říká cyklus.

Pozn.: Protože pracujeme pouze s obyčejnými grafy, posloupnost (v0,e1,v1,e2,...,vk-1,ek,vk) budeme zapisovat (v0,v1,...,vk-1,vk).

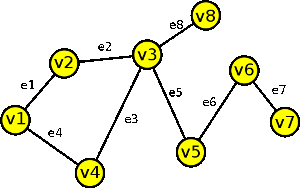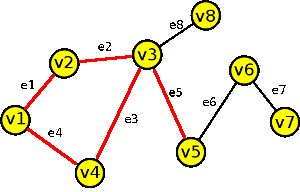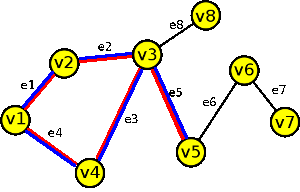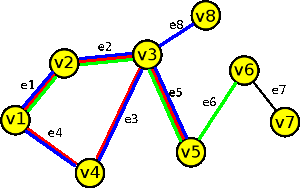	sled S = (v5,e5,v3,e3,v4,e4,v1,e1,v2,e2,v3,e5,v5)
	tah T = (v5,e5,v3,e3,v4,e4,v1,e1,v2,e2,v3,e8,v8)
	cesta P = (v1,e1,v2,e2,v3,e5,v5,e6,v6)

příklad sledu, tahu a cesty v grafu

Jednoduché shrnutí:

sled obsahuje libovolný počet libovolných vrcholů a hran
tah neobsahuje žádnou hranu dvakrát
cesta neobsahuje žádný vrchol dvakrát
kružnice neobsahuje žádný vrchol dvakrát a začíná a končí ve stejném vrcholu

Tvrzení:: V grafu G existuje cesta z vrcholu v do vrcholu w právě tehdy, když v grafu G existuje sled z vrcholu v do vrcholu w.

Důkaz:

⇒ Důkaz tvrzení plyne ihned z definice, neboť každá cesta je zároveň sled.
⇐ Zřejmě sled z vrcholu v do vrcholu w, který má nejmenší možnou délku, je již nutně cesta.∎

Dokážeme to s využitím důkazu sporem:

Nechť Smin = (v=v0,e1,v1,...,ek,vk=w) je sled minimální délky z vrcholu v do vrcholu w. Tvrdíme, že Smin je cesta z vrcholu v do vrcholu w.

Předpokládejme pro spor, že Smin je sled minimální délky z vrcholu v do vrcholu w>a zároveň Smin není cesta z vrcholu v do vrcholu w.

Jestliže Smin není cesta, znamená to, že Smin obsahuje alespoň jeden vrchol x, který se v Smin vyskytuje alespoň dvakrát, tj. Smin = (v,...,x,...,ex,x,...,w). Pak ale sled Smin - (x...,ex) je také sled z vrcholu v do vrcholu w, ale je kratší délky než Smin, což je spor s předpokladem.∎

Definice souvislosti:

Hovoříme, že v grafu G vrcholy v a u souvisí,právě když existuje v-u sled (v-u cesta) v G. Graf G je souvislý, když v něm existuje sled (cesta) mezi libovolnou dvojicí vrcholů, tj. když libovolné dva vrcholy souvisí v G.

Jednoduše vyjádřeno: z kteréhokoliv vrcholu se po hranách dostaneme do libovolného jiného vrcholu.

Definice komponenty:

Komponenta souvislosti grafu G je každý maximální souvislý podgraf grafu G.

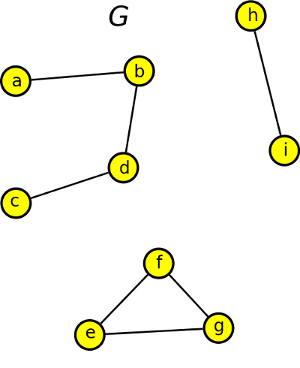
komponenta

Graf G má tři komponenty souvislosti

Příklad

Kolik komponent má graf s deseti vrcholy stupně 5?

Má-li každý vrchol stupeň 5, musí být spojen hranou s pěti dalšími vrcholy. Každý vrchol tedy leží v podgrafu o minimálně šesti vrcholech. Není tedy možné rozdělit graf o deseti vrcholech na dvě nebo více komponent, kdy každá bude mít minimálně šest vrcholů. Proto má tento graf pouze jednu komponentu a je tudíž souvislý.

Tvrzení:: Nechť graf G je souvislý a nechť obsahuje kružnici C. Pak graf G - e, kde e je libovolná hrana kružnice C, je také souvislý.

Důkaz přímo:

Nechť e = {v,w} je libovolná hrana kružnice C. Označme P = C-e cestu z vrcholu v do vrcholu w. Protože graf G je souvislý, existuje v něm mezi každými dvěma vrcholy x,y cesta Pxy, přičemž cesta Pxy buď:

neobsahuje hranu e, pak je zároveň cestou v grafu G–e nebo
obsahuje hranu e. V tom případě hranu e nahradíme cestou P, čímž získáme sled z vrcholu x do vrcholu y v grafu G, který je zároveň sledem z vrcholu x do vrcholu y i v grafu G–e.

Odtud a podle tvrzení „V grafu G existuje cesta z vrcholu v do vrcholu w právě tehdy, když v G existuje sled z vrcholu v do vrcholu w.“, existuje cesta z vrcholu x do vrcholu y v grafu G–e.

V obou případech dostáváme, že v G–e existuje cesta z vrcholu x do vrcholu y (pro libovolné vrcholy x,y), což znamená, že graf G-e je souvislý.∎

Rozlišujeme pojmy nejmenší a minimální

Tvrzení, že prvek x má nejmenší hodnotu, znamená, že každý jiný uvažovaný prvek má hodnotu větší než x. Tvrzení, že prvek x nabývá minimální hodnotu, znamená, že žádný jiný uvažovaný prvek nemá hodnotu menší než x. Obdobně chápeme rozdíl mezi pojmy největší a maximální.

Definice artikulace/mostu:

Hranu e grafu G nazýváme mostem, jestliže graf G-e má více komponent než graf G. Vrchol v grafu G nazýváme artikulací, jestliže graf G-v má více komponent než graf G.

Most je hrana, artikulace vrchol, který když z grafu odstraníme, rozpadne se graf na více komponent.

Z uvedené definice plynou například následující zřejmá tvrzení:

Každý koncový vrchol mostu stupně většího než jedna je artikulací.
Vrcholy stupně jedna a stupně nula nikdy artikulací být nemohou.
Vrchol, který je artikulací, nemusí být koncovým vrcholem mostu.
Vyjmutím mostu zvětšíme počet komponent právě o jednu.
Vyjmutím artikulace v můžeme počet komponent zvětšit o více než jednu, maximálně však o číslo rovnající se degG(v)–1.

Tvrzení:

Nechť e je most v G a p je počet komponent G, pak G-e má p+1 komponent.
Nechť v je artikulace G a p je počet komponent G, pak G-v má p´ komponent, kde p+1 ≤ p´ ≤ p+degGv-1.

Příklad

Najděte v následujícím grafu most a artikulaci.

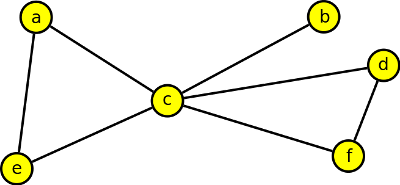
Most je hrana b-c - vzniknou dva podgrafy:

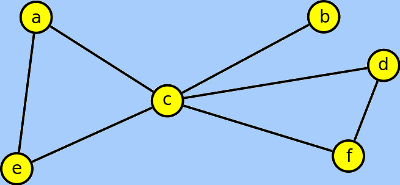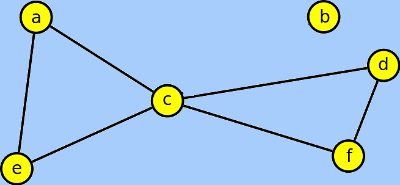
Aktikulací je vrchol c - vzniknou tři podgrafy:

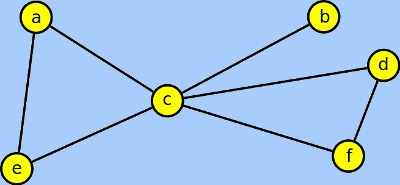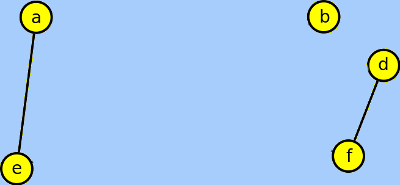
Definice vzdálenosti:

Nechť G=(V,E) je souvislý graf a nechť u,v∈V(G). Pod vzdáleností vrcholů u,v rozumíme délku nejkratší u-v cesty.

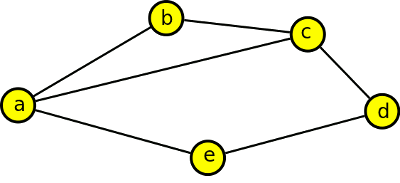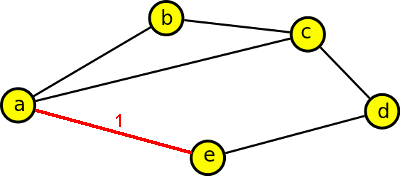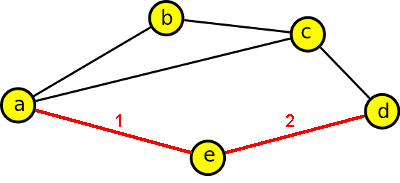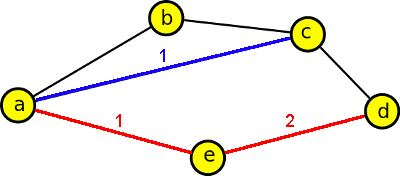
vzdálenost

Vzdálenost a,d je 2, vzdálenost a,c je 1

Jedná se vlastně o minimální počet hran, které musíme projít z jednoho vrcholu do druhého. Mezi vrcholy a,d existují celkem tři cesty - abcd, acd a aed velikostí 3,2,2. Nejkratší vzdálenost je tedy 2. Mezi vrcholy a,c existují rovněž tři cesty - ac, abc a aedc o velikostech 1,2,3. Nejkratší vzdálenost je tedy 1.

Definice izomorfismu:

Dva grafy G=(V,E) a G´=(V´,E´) nazveme izomorfní, když existuje jednoznačné zobrazení f:V→V´ takové, že platí {x,y}∈E právě tehdy, když {f(x),f(y)}∈E´ . Zobrazení f nazýváme izomorfizmus grafů G a G´. Fakt, že G a G´ jsou izomorfní, zapisujeme G≅G´.

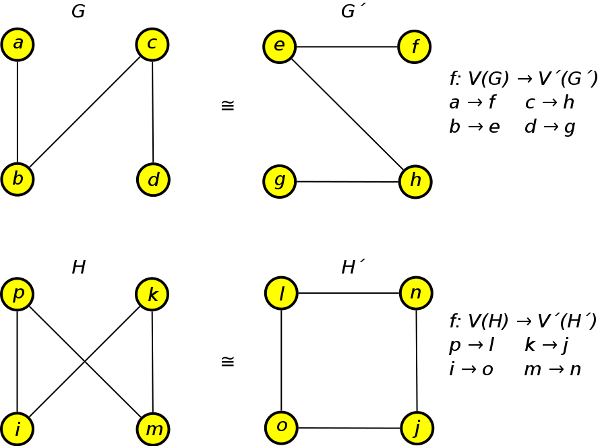
izomorfizmus

příklady izomorfních grafů

Izomorfní grafy musejí mít stejný počet vrcholů a hran. Z odpovídajících vrcholů musí vest stejný počet hran.

I když grafy budeme obvykle znázorňovat obrázkem, pro počítačové zpracování se nejčastěji používá implementace pomocí matice sousednosti, incidenční matice nebo seznamu sousedních vrcholů. Proto si nyní ukážeme, jak se grafy právě pomocí těchto matic a seznamu sousedních vrcholů zobrazují:

Definice matice sousednosti:

Nechť G=(V,E) je graf, V={v1,v2,...,vn}, pak matice sousednosti grafu G je čtvercová matice AG=(aij) typu (n×n) definovaná předpisem:

aij=1 pro {vi,vj}∈E(G)

aij=0 pro {vi,vj}∉E(G).

Pozorování:

AG je symetrická matice, tj. aij=aji, přičemž na hlavní diagonále jsou 0. Mimo diagonály buď 0 nebo 1.

Graf G

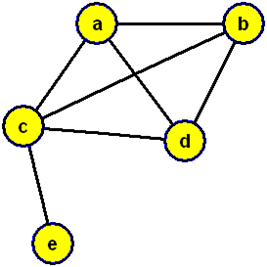
graf G

Matice sousednosti A(G) grafu G:

	a	b	c	d	e
a	0	1	1	1	0
b	1	0	1	1	0
c	1	1	0	1	1
d	1	1	1	0	0
e	0	0	1	0	0

Prostě, pokud jsou vrcholy spojeny hranou, je tam 1 jinak 0.

Seznam sousedních vrcholů

Seznam sousedních vrcholů vytvoříme tak, že na jednotlivé řádky si vypíšeme všechny vrcholy grafu a za ně vrcholy, s kterými je daný vrchol incidentní. Tyto vrcholy oddělujeme čárkou.

Seznam sousedních vrcholů k jednotlivým vrcholům grafu G:

a	-	b,	c,	d
b	-	a,	c,	d
c	-	a,	b,	d,	e
d	-	a,	b,	c
e	-	c

Příklad

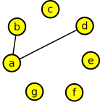
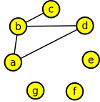
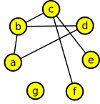
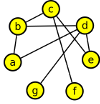
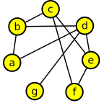
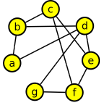
Nakreslete graf zadaný seznamem sousedních vrcholů:

A	-	B,	D,			E	-	D,	C,	F,
B	-	A,	C,	D,		F	-	C,	E,	G,
C	-	B,	E,	F,		G	-	D,	F,
D	-	A,	B,	E,	G,

Nakreslit takový graf by nemělo být problém:

Věta:

Položme $A_{G}^{(1)} = A_{G}, A_{G}^{(k)} = A_{G}^{(k - 1)} \cdot A_{G}^{(1)}$ . Pak platí:

Prvek $a_{i j}^{(k)}$ matice $A_{G}^{(k)}$ určuje počet různých vi-vj sledů délky k v grafu G.
$a_{i i}^{(2)} = \deg_{G} v_{i}$ .
Když $a_{ij}^{(n - 1)} \neq 0$ pro každou dvojicí i,j, i,j∈{1,2,3,...,n}, pak graf G je souvislý.

matice

Podle věty a) o maticích v grafu G existuje 6 a-a sledů délky 3, tu jsou:

a 4 c-e sledy délky 3, tu jsou:

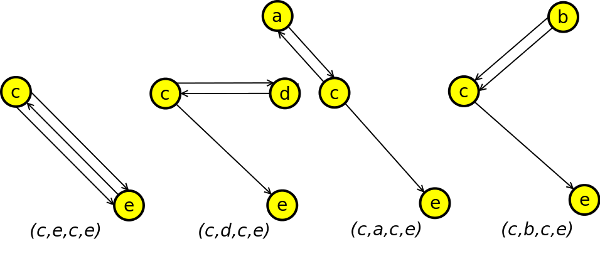
Podle věty b) o maticích platí:

dega=a1,1=3, degb=a2,2=3, degc=a3,3=4, degd=a4,4=3, dege=a5,5=1.

Platí $a_{ij}^{(4)} \neq 0$ pro každou dvojicí i,j, i,j∈{1,2,3,4,5}, podle věty c) je graf G souvislý.

Příklad

Zapište matici sousednosti pro následující graf.

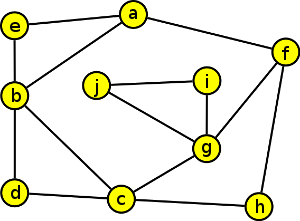
Nejprve vytvoříme prázdnou matici, kde nahoře a vlevo zapíšeme označení všech vrcholů grafu:

	a	b	c	d	e	f	g	h	i	j
a
b
c
d
e
f
g
h
i
j

Potom zapíšeme 1 do průsečíku těch vrcholů, mezi kterými existuje hrana:

	a	b	c	d	e	f	g	h	i	j
a		1			1	1
b	1		1	1	1
c		1		1			1	1
d		1	1
e	1	1
f	1						1	1
g			1			1			1	1
h			1			1
i							1			1
j							1		1

Definice incidenční matice:

Pro neorientovaný graf G=(V,E) s n vrcholy a m hranami je to n×m matice.

$M = (m_{i, j})$ , kde $m_{i, j}$ je $\{\begin{matrix} 1, když e_{j} je incidentní s v_{j} \\ 0 jinak \end{matrix}$

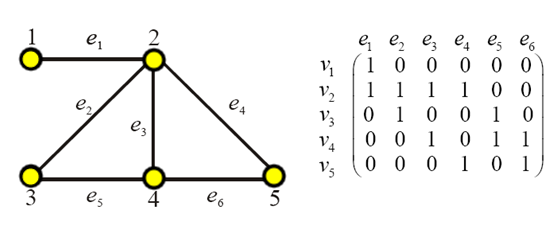
graf a jeho incidenční matice

Rozdíl v maticích je ten, že matice sousednosti obsahuje v řádku i sloupci vrcholy a jednička v průsečíku znamená, že vrcholy jsou spojeny hranou. Incidenční matice obsahuje v popisu řádků vrcholy a v popisu sloupců hrany a jednička znamená, že hrana je incidentní s vrcholem.

Definice doplňku (=komplementu):

Graf $\bar{G} = (V, \bar{E})$ je doplněk grafu G=(V,E) když hrana $\{v_{i}, v_{j}\} \in \bar{E}$ tehdy a jenom tehdy, když {vi,vj}∉E. Jinými slovy, dva vrcholy vi,vj jsou sousední v $\bar{G}$ právě tehdy, když nejsou sousední v G. (Také se můžeme setkat s označením doplňku: –G=(V,-E).)

Graf a jeho doplněk

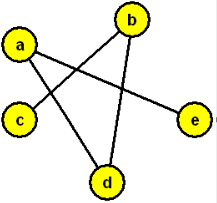
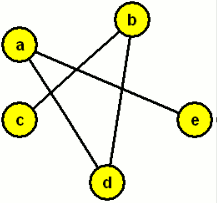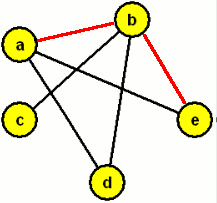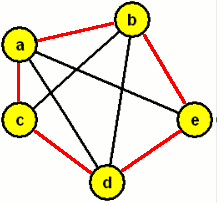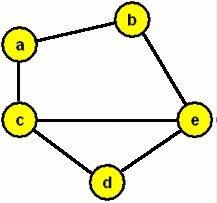
graf H doplněk H

Opět zjednodušeně: Položíme-li graf a jeho doplněk na sebe, dostaneme kompletní graf.

Příklad

Nakreslete doplňky (komplementy) grafů:

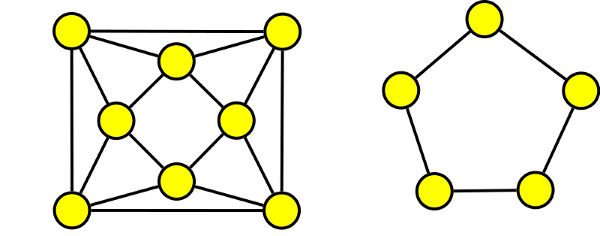
grafy

Doplňky grafů jsou:

doplňky grafů

Definice grafové posloupnosti:

Každému grafu G=(V,E) s V={v1,v2,...,vn} můžeme jednoznačně přiřadit posloupnost stupňů ${\{s_{i}\}}_{i =1}^{n}$ , kde si=degvi. Obráceně se můžeme ptát: „Je daná posloupnost přirozených čísel {di}ni=1. Existuje takový n- vrcholový graf G, aby pro jeho posloupnost stupňů platilo si=degvi=di, pro každé i=1,2,...,n? Jestliže ano, tak posloupnost {di}ni=1 nazveme grafová posloupnost = skóre grafu.

Veta o grafové posloupnosti (o skóre grafu):

Nechť D=(d1,d2,…dn) je posloupnost přirozených čísel. Předpokládejme, že d1≤d2≤…≤dn, a označme symbolem D’ posloupnost (d1’,d2’,…dn-1’), kde

di’=di pro i<n-dn

di’=di-1 pro Xi ≥n-dn.

Potom D je skóre grafu právě když D’ je skóre grafu.

Důkaz této věty je obtížnější, zájemci jej najdou např. v knize Matoušek, J., Nešetřil, J.: Kapitoly z diskrétní matematiky, Karolinum, Praha, 2000 (str. 111- 112).

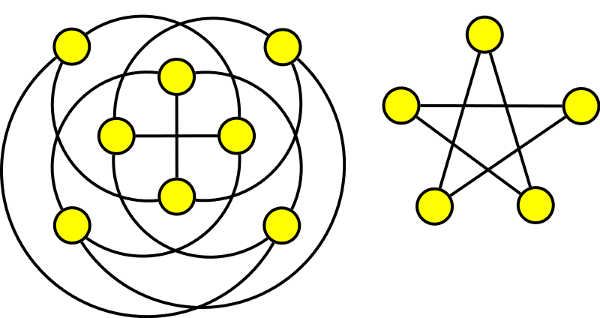
Příklad

Určete, zda posloupnost (0,1,1,1,1,1,2,2,2,4,5) je skóre grafů. Když ano, nakreslete dva navzájem neizomorfní grafy s příslušným skóre.

Budeme postupovat tak, že stupně jednotlivých vrcholů seřadíme vzestupně. Potom z posloupnosti odebereme vrchol s nejvyšším stupněm a od tolika dalších vrcholů zprava, jaký měl tento vrchol stupeň, odebereme 1.

Toto budeme opakovat tak dlouho, dokud nebude zřejmé, že se jedná nebo nejedná o posloupnost grafu.

D = (0,1,1,1,1,1,2,2,2,4,5) → D´ = (0,1,1,1,1,0,1,1,1,3) ≈ D´ = (0,0,1,1,1,1,1,1,1,3) → D´´ = (0,0,1,1,1,1,0,0,0) ≈ D´´ = (0,0,0,0,0,1,1,1,1) → D´´´ = (0,0,0,0,0,1,1,0) ≈ D´´´ = (0,0,0,0,0,0,1,1) → D´´´´ = (0,0,0,0,0,0,0) ... (0,0,0,0,0,0,0) je skóre, protože k dané posloupnosti existuje graf. Jde o graf se sedmi izolovanými vrcholy ⇨ podle věty o skóre grafu, je posloupnost (0,1,1,1,1,1,2,2,2,4,5) skóre grafu.

Začneme s kreslením. Nejprve nakreslíme graf podle poslední posloupnosti D´´´´ = (0,0,0,0,0,0,0). Nakreslíme tedy sedm vrcholů stupně 0.

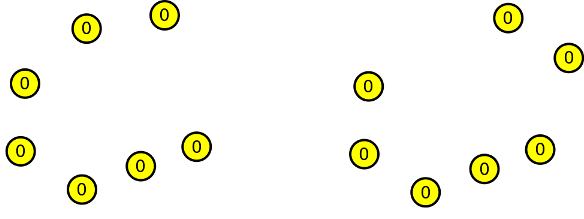
Podle D´´´ = (0,0,0,0,0,0,1,1) přidáme poslední odebraný vrchol a vedeme od něho jednu hranu k libovolnému vrcholu. Tím nám vzniknou dva vrcholy stupně 1.

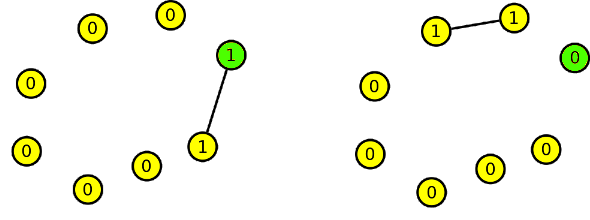
Podle D´´ = (0,0,0,0,0,1,1,1,1) přidáme další vrchol a opět od něho vedeme jednu hranu. Tentokrát si ale musíme vybrat vrchol, který má ještě stále stupeň 0. Tím nám vzniknou čtyři vrcholy stupně 1, přesně podle skóre grafu D´´.

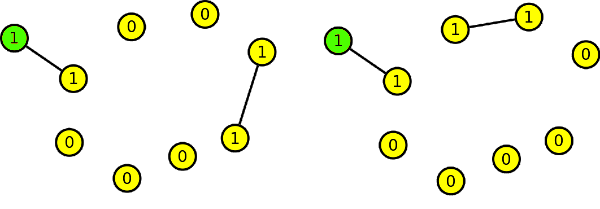
Další přidaný vrchol podle D´ = (0,0,1,1,1,1,1,1,1,3) je stupně 3. Přidáme ho tedy do grafu a vedeme od něho tři hrany k vrcholům se stupněm 0, protože jak vidíme ze skóre, přibudou nám ještě tři vrcholy se stupněm 1.

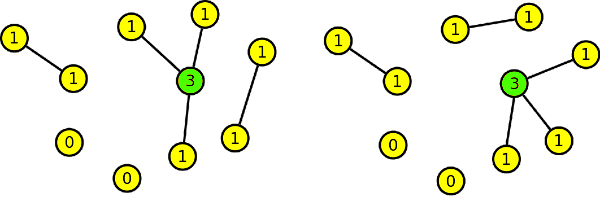
Nakonec přidáme podle D = (0,1,1,1,1,1,2,2,2,4,5) vrchol, který jsme odebrali jako první. Tento vrchol je stupně 5, proto od něho vedeme pět hran. Jednu hranu vedeme k vrcholu stupně 3, aby nám vznikl vrchol stupně 4, tři hrany k vrcholům stupně 1. Tím nám vzniknou požadované tři vrcholy stupně 2. Poslední hranu vedeme k libovolnému vrcholu stupně 0, aby nám vznikl vrchol stupně 1.

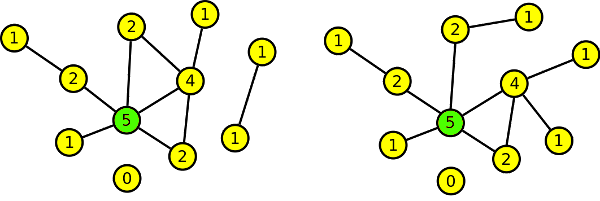
Tento postup můžeme s úspěchem použít jako univerzální pro kreslení grafů ze zadané posloupnosti. Neizomorfismu grafů jsme dosáhli porušením sousednosti. Vrchol stupně 4 sousedí v prvním grafu s dvěma vrcholy stupně 2, kdežto v druhém grafu pouze s jedním.

Řešený příklad ⇫

1. Nakreslete dva neizomorfní grafy se skóre (1,1,1,1,2,3,3):

Krok 1

nejprve nakreslíme vrcholy grafu. Ze skóre vidíme, že je jich sedm:

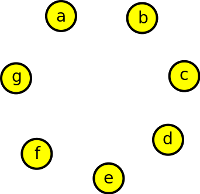
Krok 2

podle skóre doplníme hrany a jeden graf by mohl vypadat například takto:

Krok 3

posuneme jednu hranu tak, aby nebyly dva sousední vrcholy stupně tři a další graf může vypadat takto:

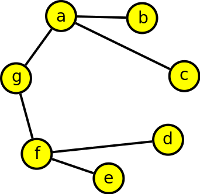
Grafy nejsou izomorfní, protože v prvním grafu jsou vrcholy stupně 3 sousední, kdežto v druhém ne.

2.Existují dva neizomorfní grafy se 6 vrcholy stupňů 2?

Krok 1

Graf, který má vrcholy stupně 2 je vlastně kružnice.

Krok 2

Zbývá tedy zjistit, kolik různých kružnic můžeme na šesti vrcholech vytvořit.

Krok 3

Jelikož nejmenší kružnice má tři vrcholy, můžeme vytvořit buď jednu kružnici se šesti vrcholy nebo dvě kružnice po třech vrcholech. Z toho jasně vyplývá, že dva neizomorfní grafy můžeme vytvořit .

3.Kolik hran má graf s osmi vrcholy stupně 4?

Krok 1

z každého z osmi vrcholů vedou čtyři hrany, to jest 8∙4=32

Krok 2

musíme si ale uvědomit, že například hrana ab je stejná jako ba, proto musíme výsledk vydělit dvěma

Krok 3

32:2=16, graf má tedy 16 hran.

4. Který graf má více hran. K6,6 nebo K9?

Krok 1

nejprve určíme počet hran grafu K6,6. Má 12 vrcholů, každý má stupeň 6. 12∙6:2=36. K6,6 má 36 hran.

Krok 2

počet hran K9 je 9∙8:2=36. K9 má 36 hran.

Krok 3

můžeme prohlásit, že tyto dva grafy mají stejný počet hran.

5. Nakreslete graf se stupňovou posloupností (0,0,1,1,2,2,3,3,4,4).

Krok 1

z posloupnosti vidíme, že máme 10 vrcholů. Nakreslíme si je tedy.

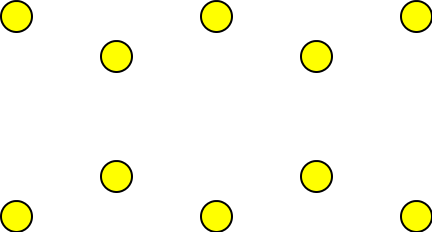
vrcholy

Krok 2

z posloupnosti odebereme jeden vrchol s nejvyšším stupněm a posloupnost upravíme. Odebereme 4 a dostaneme posloupnost (0,0,1,1,1,2,2,2,3)

Krok 3

opět odebereme nejvyšší stupeň, tj. 3 a dostaneme (0,0,1,1,1,1,1,1) a tento graf již dokážeme nakreslit.

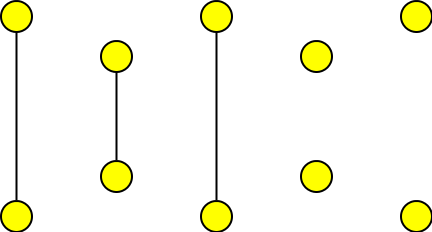
první krok

Krok 4

přidáme odebraný vrchol stupně 3

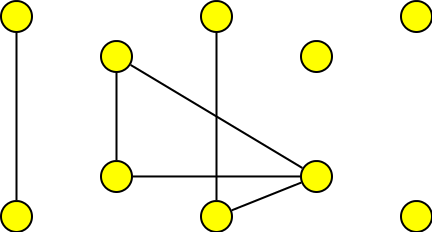
druhý krok

Krok 5

nakonec přidáme odebraný vrchol stupně 4 a graf dokreslíme

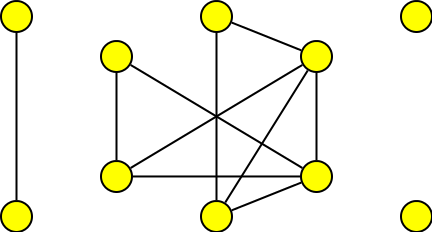
hotový graf

Pokud porovnáte postup kreslení grafu s příkladem u definice grafové posloupnosti, vidíte, že je možná konstrukce grafu dvěma způsoby. Buď postupně přidáváme vrcholy a hrany nebo nakreslíme všechny vrcholy a pak přidáváme podle posloupnosti již jen hrany.

6. Je dána množina čísel M={1,2,3,4,5,6}. Znázorněte přehledně soudělitelnost čísel z této množiny.

Krok 1

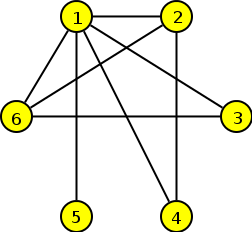
soudělitelnost čísel

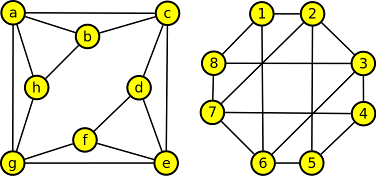
7. Najděte mezi následujícími grafy všechny izomorfní dvojice a zdůvodněte svou odpověď.

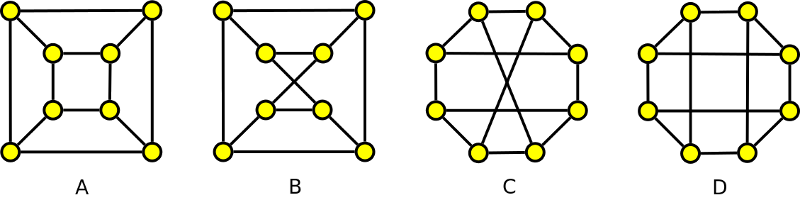
Krok 1

Izomorfní grafy musí mít stejný počet vrcholů a hran. Rovněž skóre musejí mít stejné.

Krok 2

Výše uvedené nám bohužel nijak nepomohlo, neboť počty vrcholů i skóre mají všechny grafy stejné. Proto musíme hledat dále. Zkontrolujeme tedy například vzdálenosti mezi jednotlivými vrcholy.

Krok 3

Vzdálenost mezi libovolnými dvěma vrcholy v grafu A je max. 3, v grafu B je max. 2, v grafu C je max. 2 a v grafu D je to to opět max.3. Z uvedeného vyplývá, že by mohly být izomorfní grafy A, D a B, C.

Krok 4

A skutečně izomorfní jsou. Přesuneme-li vnitřní vrcholy grafu A vně, dostaneme graf D a to stejné platí i pro graf B a C.

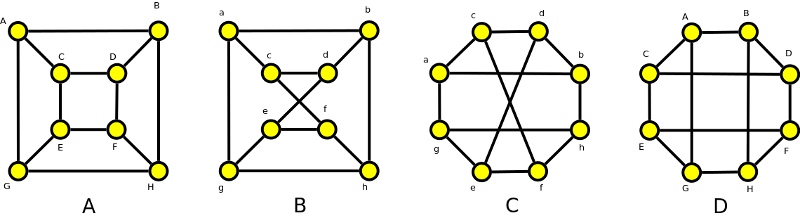
označeny jsou odpovídající si vrcholy

8. Nakreslete takový graf, který obsahuje most a neobsahuje artikulaci.

Krok 1

Jelikož víme, že jediný vrchol mostu, který zároveň není aktikulací, je vrchol stupně 1, můžeme nakreslit pouze takovýto graf:

Krok 2

9. Nakreslete takový graf, který neobsahuje most a obsahuje artikulaci.

Krok 1

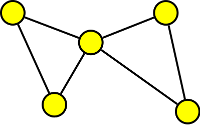
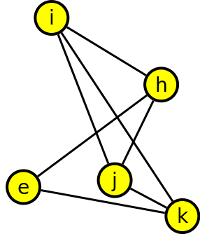
10. Určete:

cestu délky 4 začínající ve vrcholu b,
tah délky 7, který není cesta,
mosty a artikulace,
podgraf, který obsahuje kružnici délky 5,
podgraf indukovaný vrcholy e,h,j,k,i a k tomuto podgrafu nakreslete jeho doplněk.

Krok 1

Cesta je takový sled, ve kterém se nevyskytují ani vrcholy, ani hrany, dvakrát a je otevřený. Takže cesta délky 4 začínající ve vrcholu b může být například: b,i,d,e,f nebo b,f,d,e,j.

Krok 2

Tah je sled, ve kterém se neopakuje žádná hrany. Tah délky 7 je například: b,i,d,e,f,b,e,j.

Krok 3

Mosty jsou hrany a aktikulace vrcholy, po jejichž odebrání se zvýší počet komponent grafu. Most jsou tedy hrany: a-c, e-j. Artikulací je pouze vrchol e.

Krok 4

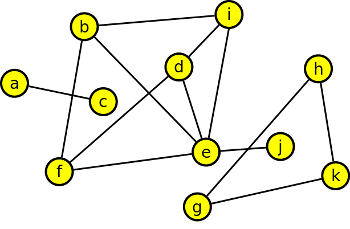
Podgraf, který obsahuje kružnici délky 5 je například podgraf: b,d,e,f,i,j a kružnice je například b,i,d,e,f,b.

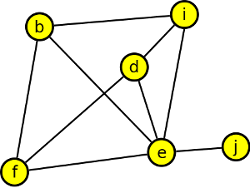
Krok 5

Indukovaný podgraf e,h,j,k,i je tento:

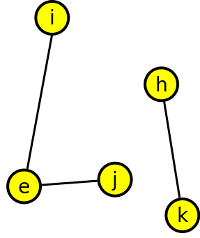
a jeho doplněk je tento:

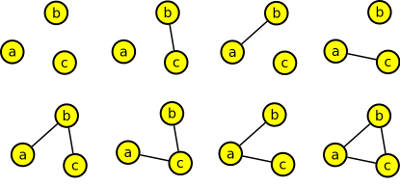
11. Nakreslete všechny grafy na třech vrcholech a,b,c.

Krok 1

Graf, který má tři vrcholy, může mít tři, dvě, jednu nebo žádnou hranu. Takové grafy není těžké nakreslit:

Krok 2

12. Kolik existuje všech obyčejných grafů na n vrcholech?.

Krok 1

Uvědomme si, jaký maximální počet hran může graf mít. Vrcholů je n a každý má stupeň n-1 ⇒ počet hran je tedy n(n-1). Takto je ale každá hrana počítána dvakrát, proto musíme výraz ještě vydělit 2. Počet hran je $\frac{n (n - 1)}{2} = (\begin{matrix} n \\ 2 \end{matrix})$

Krok 2

Každá hrana v n-vrcholovém grafu může nabýt dva stavy. Buď hrana v grafu je nebo není - 1 nebo 0. Abychom zjistili, kolik grafů existuje na n vrcholech, stačí vypočítat, kolik existuje všech variací s opakováním, kde vybíráme $(\begin{matrix} n \\ 2 \end{matrix})$ -tici z dvouprvkové množiny {0,1}. Těch je: $2^{(\begin{matrix} n \\ 2 \end{matrix})} = 2^{\frac{n (n - 1)}{2}}$

13. Zjistěte, zda následující posloupnost je skóre grafu. Když ne, zdůvodněte proč, když ano, nakreslete příslušný graf: (7,6,6,6,3,3,3,2), (6,5,4,3,3,2,1).

Krok 1

Nejprve uspořádáme posloupnost vzestupně, abychom splnily předpoklad věty: D=(7,6,6,6,3,3,3,2)≈D=(2,3,3,3,6,6,6,7).

Krok 2

Vždy odečteme poslední stupeň a výslednou posloupnost opět vzestupně seřadíme: D=(2,3,3,3,6,6,6,7)→ D´=(1,2,2,2,5,5,5).

Krok 3

D´=(1,2,2,2,5,5,5)→D´´=(1,1,1,1,4,4)

Krok 4

D´´=(1,1,1,1,4,4)→D´´´=(1,0,0,0,3)≈D´´´=(0,0,0,1,3)

Krok 5

D´´´=(0,0,0,1,3)→D´´´´=(0,-1,-1,0)...nemusíme uspořádávat, jelikož je zřejmé, že se nejedná o skóre grafu, protože nemůžeme mít vrchol se záporným stupněm.

Krok 6

Opět podle věty nejprve uspořádáme a potom postupně odebereme vrchol s nejvyšším stupněm. D=(6,5,4,3,3,2,1)≈D=(1,2,3,3,4,5,6)→D´=(0,1,2,2,3,4)→D´´=(0,0,1,1,2)

Krok 7

Vidíme, že D´´=(0,0,1,1,2) je skóre grafu, neboť tento graf již dokážeme nakreslit.

Krok 8

S kreslením grafu začneme od posloupnosti D´´=(0,0,1,1,2):

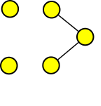
pokračujeme posloupností D´=(0,1,2,2,3,4):

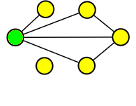
až skončíme posloupností D=(1,2,3,3,4,5,6):

14. Z matice sousednosti určete:

skóre grafu
počet vrcholů a hran (ze skóre)
podgraf indukovaný vrcholy b,d,e,f,i

	a	b	c	d	e	f	g	h	i	j	k
a			1
b				1	1	1			1
c	1
d		1			1	1			1
e		1		1		1			1	1
f		1		1	1
g								1			1
h							1				1
i		1		1	1
j					1
k							1	1

Krok 1

Zapsat grafou posloupnost (skóre grafu) z matice sousednosti je poměrně jednoduché. Jednoduše po řádcích zapisujeme počty jedniček v daném řádku: (1,4,1,4,5,3,2,2,3,1,2). Nakonec můžeme zapsat skóre grafu D=(1,1,1,2,2,2,3,3,4,4,5).

Krok 2

Počet vrcholů ze skóre grafu zjistíme tak, že pouze sečteme počet hodnot v grafové posloupnosti. V našem případě to je jedenáct.

Krok 3

K zjištění počtu hran využijeme Větu o principu sudosti. Sečteme tedy všechny stupně a výsledek vydělíme 2. 1+1+1+2+2+2+3+3+4+4+5=28, 28:2=14. Počet hran tohoto grafu je tedy 14.

Krok 4

Graf budeme kreslit tak, že z matice vybereme pouze požadované vrcholy a hrany mezi nimi, tj. b,d,e,f,i. Pro přehlednost si můžeme zapsat seznam sousedních vrcholů:

b	-	d,	e,	f,	i,	f	-	b,	d,	e,
d	-	b,	e,	f,	i,	i	-	b,	d,	e,
e	-	b,	d,	f,	i,

Nakreslíme si pět vrcholů:

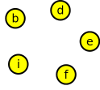
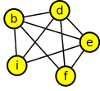
...a dokreslíme hrany:

15. Manželé Novotní šli na večírek, kde se setkali se třemi dalšími manželskými páry. V průběhu večerah vyměnili své vizitky, přičemž si ji nevyměnil se svým partnerem, a nikdo nedal více vizitek téže osobě. Před odchodem napadlo pana Novotného zeptat se každého, s kolika osobami si dotyčný vyměnil vizitku. Ke svému překvapení dostal od každého jinou odpověď. S kolika lidmi si vyměnila vizitku paní Novotná?

Krok 1

Sestavíme si skóre grafu.

Uvažujme takto: manželů bylo celkem osm, takže budeme mít graf o osmi vrcholech. Předání vizitky označíme hranou. Maximální stupeň vrcholu bude 6, protože nikdo nedal vizitku svému partnerovi. Vytvoříme skóre, které bude mít osm prvků, kde každý by měl mít jinou hodnotu, ale nejvyšší hodnota by měla být 6. Takové skóre ovšem nejde vytvořit, ale... Všichni odpověděli panu Novotnému jinak, takže sedm vrcholů musí mít jiný stupeň (nikde není řečeno, že pan Novotný si nevyměnil stejný počet vizitek jako někdo jiný).

Takové posloupnosti už zapsat dokážeme. Zde jsou: (0,0,1,2,3,4,5,6), (0,1,1,2,3,4,5,6), (0,1,2,2,3,4,5,6), (0,1,2,3,3,4,5,6), (0,1,2,3,4,4,5,6), (0,1,2,3,4,5,5,6), (0,1,2,3,4,5,6,6).

Krok 2

Pokusíme se určit, které z vytvořených posloupností jsou skóre grafu.

Posloupnosti (0,0,1,2,3,4,5,6), (0,1,2,2,3,4,5,6), (0,1,2,3,4,4,5,6), (0,1,2,3,4,5,6,6) můžeme hned podle Věty o principu sudosti vyřadit.

Krok 3

U ostatních posloupností musíme určit, zda je to skóre grafu klasicky.

(0,1,1,2,3,4,5,6)→(0,0,0,1,2,3,4)→(0,0,-1,0,1,2)⇒není to skóre grafu
(0,1,2,3,3,4,5,6)→(0,0,1,2,2,3,4)→(0,0,0,1,1,2)⇒je to skóre grafu
(0,1,2,3,4,5,5,6)→(0,0,0,1,2,3)→(0,0,-1,0,1)⇒není to skóre grafu

Vidíme, že pouze jedna posloupnost je i skóre grafu - (0,1,2,3,3,4,5,6). Z této posloupnosti vidíme, že máme dva vrcholy stupně 3. Pan Novotný si tedy musel vyměnit vizitku se třemi osobami.

Krok 4

Nyní nakreslíme podle posloupnosti graf o osmi vrcholech. Vrcholy jsou označeny takto: Novotní: 1a,1b. Ostatní páry mají označení obdobné: 2a,2b, 3a,3b, 4a,4b.

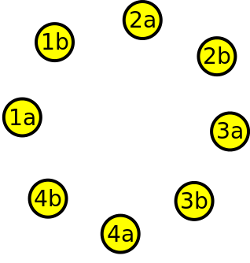
Krok 5

Z libovolného vrcholu (nesmí to být vrchol pana Novotného - 1a, protože ten má stupeň 3) vedeme šest hran tak, že vynecháme hranu k partnerovi.

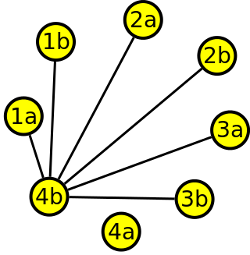
Krok 6

Nyní přidáme k dalšímu vrcholu čtyři hrany, aby nám vznikl vrchol stupně 5. Musíme ale myslet na to, že nám musí zbýt vrchol stupně 0 a vrchol stupně 1 a nesmíme propojit vrcholy v páru.

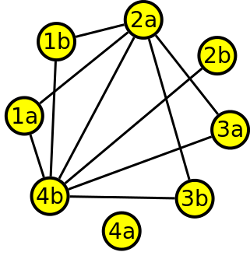
Krok 7

Nakonec potřebujeme vytvořit vrchol stupně 4. Přidáme proto k libovolnému vrcholu stupně 2 další dvě hrany tak, abychom nepropojili partnerský vrchol.

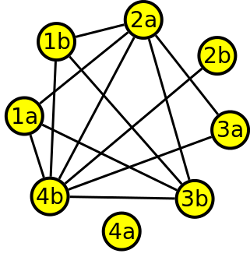
Podle výsledného grafu můžeme tedy prohlásit, že paní Novotná si vyměnila vizitku se třemi osobami.

Můžeme ale postupovat i jinak. Například podle úvahy:

Vrchol stupně 6 může být v partnerství pouze s vrcholem stupně 0, protože do ostatních vrcholů vede hrana (vyměnil si vizitku), vrchol 5 může být v partnerství s vrcholem 1, vrchol 4 s vrcholem 2 a vrchol 3 s vrcholem 3. Když víme, že pan Novotný je stupně 3, tak paní Novotná je také stupně 3.

16. Vyvraťte tvrzení: ∀G=(V,E): každý vrchol grafu G leží na kružnici ⇒ graf G je souvislý.

Krok 1

Provedeme negaci věty: ∃G=(V,E): každý vrchol grafu G leží na kružnici ⋀ graf G není souvislý

Krok 2

Jelikož takovýto graf dokážeme nakreslit, platí negace. Platí-li negace, neplatí původní tvrzení.

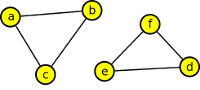
Úlohy k řešení ⇫

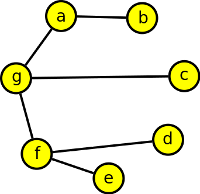
1. Detektivní kancelář (zadání převzato z časopisu Hádanka a křížovka)

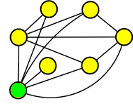
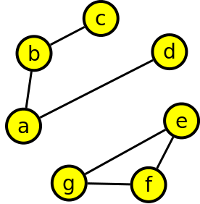
Dva detektivové zkoumali sedmičlennou skupinu osob a v grafu (každý ve svém) propojili dvojice, které se znají (nepropojené dvojice se neznají). Jeden si osoby označil čísly, druhý písmeny. Zjistěte, která písmena a čísla odpovídají stejným osobám.

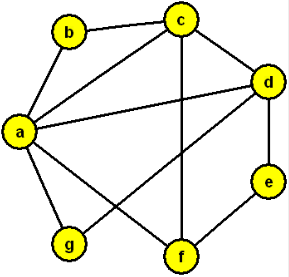
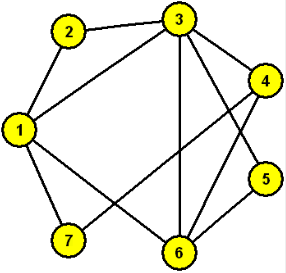
písmena čísla

Výsledek

3-a, 5-b, 6-c, 1-d, 7-e, 4-f, 2-g

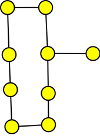
2. Nakreslete takový graf s 9 hranami, který má alespoň jeden most, ale zároveň nejvýše tři mosty, a jehož žádný podgraf není isomorfní s úplným grafem K4 a ani kružnicí délky 5. Napište jeho skóre.

Výsledek

Skóre je (1,2,2,2,2,2,2,2,3) a graf:

3. Napište stupňovou posloupnost grafu C4, K4, K3,2

Výsledek

(2,2,2,2), (3,3,3,3), (2,2,2,3,3)

4. Pro jaké n je Kn kružnicí?

Výsledek

n = 3

5. Kolik hran má graf s 11 vrcholy stupně 5?

Výsledek

takový graf neexistuje (princip sudosti)

6. Kolik hran musíme odebrat z grafu K6 , abychom dostali K3,3 ?

Výsledek

6 hran, graf K6 má 6∙5/2=15 hran a graf K3,3 má 3∙3=9 hran.

7. Najděte všechny indukované neizomorfní podgrafy grafu:

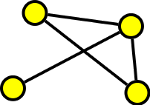
Výsledek

8. Vyvraťte tvrzení:

∀G=(V,E): V grafu G existuje kružnice C obsahující hranu e⇒G-e je souvislý graf.

Výsledek

Provedeme negaci: ∃G=(v,E): V G existuje kružnice C obsahující hranu e a zároveň G-e není souvislý graf.

Takovýto graf dokážeme nakreslit. Proto můžeme tvrdit: Negace je pravdivá, původní tvrzení nepravdivé.

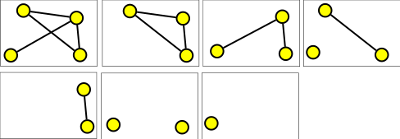
9. Zapište matice sousednosti pro následující grafy:

Graf Graf

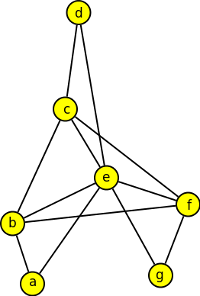
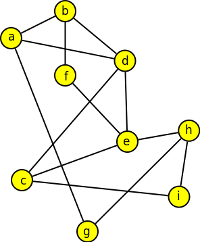
Výsledek

	a	b	c	d	e	f	g
a		1			1
b	1		1		1	1
c		1		1	1	1
d			1		1
e	1	1	1	1		1	1
f		1	1		1		1
g					1	1

	a	b	c	d	e	f	g	h	i
a		1		1			1
b	1			1		1
c				1	1				1
d	1	1	1		1
e			1	1		1		1
f		1			1
g	1							1
h					1		1		1
i			1					1

10. Nakreslete grafy podle následujících matic sousednosti:

	a	b	c	d	e	f	g	h
a		1	1
b	1
c	1			1			1	1
d			1		1	1
e				1		1
f				1	1
g			1					1
h			1				1

	a	b	c	d	e	f	g
a		1		1
b	1		1
c		1
d	1
e						1	1
f					1		1
g					1	1

Výsledek

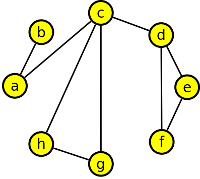
Výsledné grafy mohou vypadat například takto.

11. Kolik existuje všech obyčejných grafů na čtyřech vrcholech a,b,c,d?

Výsledek

2^{(\begin{matrix} 4 \\ 2 \end{matrix})} = 2^{\frac{4 (4 - 1)}{2}} = 2^{6} = 64

12. Určete, zda následující posloupnosti jsou skóre grafu:

(1,2,2,3,4,4,5,5)
(2,2,2,4,4)
(1,3,3,4,6,6,6)
(1,2,2,3,4,5,5)
(2,3,4,4,5,5,5)
(6,3,3,3,3,3,3)
(0,2,4,4,4,4,6)
(2,3,5,5,5,6,6)
(1,1,1,2,2,5)
(1,1,1,1,1,1,5,5)

Výsledek

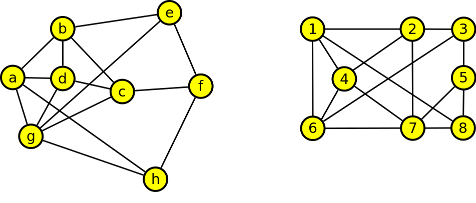
13. Rozhodněte, zda následující dvojice grafů jsou nebo nejsou izomorfními grafy:

Výsledek

nejsou izomorfní - v prvním grafu je kružnice délky 3, v druhém není
jsou izomorfní - f5,b1,d4,c6,a2,e3
nejsou izomorfní - v prvním grafu vrchol stupně 5 sousedí s dvěma vrcholy stupně 3, které nejsou sousední, v druhém sousední jsou

14. Kolik vrcholů obsahuje obyčejný graf, který má 21 hran, tři vrcholy stupně 4 a ostatní vrcholy stupně 3?

Výsledek

Graf má 13 vrcholů.

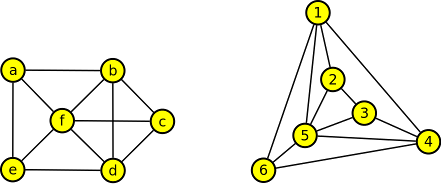
15. V grafu G najděte podgraf izomorfní s doplňkem grafu G´.

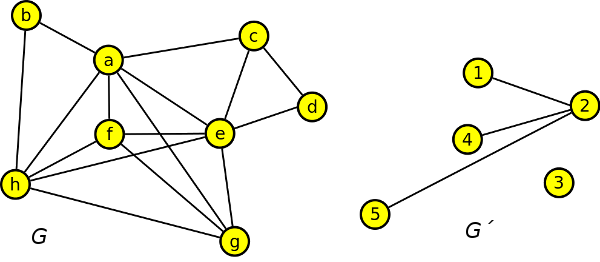
Výsledek

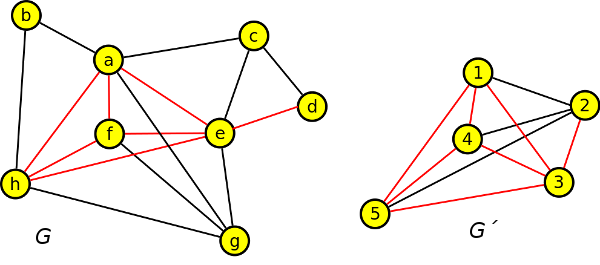
červeně je označen nalezený podgraf v garfu G a doplněk v grafu G´

16. Vyvraťte tvrzení:

∀G=(V,E): |E|≥|V| - 1 ⇒ G je souvislý

Výsledek

Negace: ∃G=(V,E): |E|≥|V| - 1 ⋀ G není souvislý

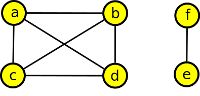
7≥6-1 platí negace, neplatí původní tvrzení.

17. Nechť p označuje počet vrcholů stupně k v grafu G, který má n-vrcholů a m-hran. Dokažte přímo, že jestliže G má pouze vrcholy stupně k a k+1, pak platí, že p = (k + 1)n – 2m.

Výsledek

Důkaz přímo:

Graf G obsahuje jenom vrcholy stupně k a k + 1. Proto platí: pro ∀vi∈G, i = 1,2,...,n deg(vi) = k ∨ deg(vi) = k+1 . Nechť vk je počet vrcholů stupně k v grafu G, pak platí vk+(n-vk)=n.

Pro každý graf platí věta – princip sudosti: $\sum_{v \in V} \deg_{G} v = 2 m$ ⇒

⇒ deg(v1)+deg(v2)+...+deg(vn)=2m ⇒ (můžeme předpokládat, že na prvních místech jsou všechny vrcholy stupně k a pak vrcholy stupně k+1)

⇒ k ⋅ vk + (k + 1) ⋅ (n − vk) = 2m ⇒

⇒ k ⋅ vk + (k + 1) ⋅ n − (k + 1) ⋅ vk = 2m ⇒

⇒ k ⋅ vk + (k + 1) ⋅ n − k ⋅ vk − vk = 2m ⇒

⇒ (k + 1) ⋅ n − vk = 2m ⇒

⇒ vk = (k + 1) ⋅ n − 2m.

18. Když δ(G)≥2, tak G obsahuje kružnici. Dokažte!

Výsledek

Důkaz přímo:

Nechť P = (v1,v1,...,vk) je maximální cesta v grafe G (t.j. cesta větší délky v G neexistuje). Délka cesty P je k-1.

Pro minimální stupeň grafu G platí: δ(G)≥2 ⇒ deg(v1)≥2 ⇒ vrchol v1 má minimálně dva sousedy. (Jedním ze sousedů je vrchol v2∈P, v1 má ještě minimálně jednoho souseda.) Platí následovní tvrzení, které také dokážeme:

Tvrzení: Všichni sousedé vrcholu v1 patří cestě P.
- Důkaz sporem: Nechť předpoklad neplatí, tj. existuje minimálně jeden vrchol u grafu G, který sousedí s v1 (tj. {u,v} ∈ E(G)) a zároveň u∉P. Pak cesta P spolu s hranou {v1,u} tvoří cestu P´ = P∪{v1,u}, které délka (je k) je větší než délka P a to je spor, protože cesta P byla v grafu G maximální. Platí původní tvrzení. ■

Z tvrzení ⇒ ∃vi ∈ P(i=3∨i=4∨...∨i=k): {v1,vi} ∈ E(G) ⇒ C=(v1,v2,...,vi)∪{vi,v1} je kružnice.

19. Dokažte sporem větu: Jestliže graf G (souvislý nebo nesouvislý) má právě 2 vrcholy lichého stupně, pak obsahuje i cestu spojující tyto dva vrcholy. (Nejprve správně zformulujte tvrzení pro důkaz sporem!)

Výsledek

Důkaz sporem:

Nechť tvrzení neplatí, pak: Nechť graf G (souvislý nebo nesouvislý) má právě 2 vrcholy lichého stupně a zároveň G neobsahuje cestu spojující tyto dva vrcholy.

G neobsahuje cestu spojující dva vrcholy lichého stupně (označme je x,y) ⇒ tyto dva vrcholy lichého stupně x,y se nenacházejí v jedné komponentě souvislosti ( vrchol x se nachází v jedné komponentě souvislosti a vrchol y se nachází v druhé komponentě souvislosti, ostatní vrcholy jsou stupně sudého) a to je spor s důsledkem věty o sudosti: každý graf má sudý počet vrcholů lichého stupně (na každou komponentu souvislosti se totiž díváme jako na graf, pro každou komponentu platí všechna tvrzení jako pro graf). Tedy předpoklad byl špatný, a proto platí původní tvrzení.

20. Kolik je indukovaných podgrafů s pěti vrcholy v K9?

Výsledek

$(\begin{matrix} 9 \\ 5 \end{matrix})$

21. Kolik je cest v K7 mezi vrcholy A a B?

Výsledek

1+5+5∙4+5∙4∙3+5∙4∙3∙2+5∙4∙3∙2∙1 = 326 cest

22. Dokažte, že když pro minimální stupeň δ(G) grafu G je δ(G) ≥ k ≥ 2, tak G obsahuje jako podgraf cestu délky alespoň k a kružnici délky alespoň k+1.

Výsledek

Důkaz přímo:

Nechť P = (v1,v2,...,vs) je maximální cesta v grafu G (t.j. cesta větší délky v G neexistuje). Délka cesty P je s-1.

Pro minimální stupeň grafu G platí: δ(G)≥k≥2 ⇒ deg(v1)≥k≥2 ⇒ vrchol v1 má minimálně k sousedů. (Jedním ze sousedů je vrchol v2∈P, v1 má ještě minimálně k-1 sousedů.) Platí následující tvrzení, které také dokážeme:

Tvrzení: Všichni sousedé vrcholu v1 patří cestě P.
- důkaz sporem: Nechť předpoklad neplatí, tj. Existuje minimálně jeden vrchol u grafu G, který sousedí s v1 (tj. {u,v1}∈E(G) ) a zároveň u∉P. Pak cesta P spolu s hranou {v1,u} tvoří cestu P´ = P∪{v1,u}, které délka (je s) je větší než délka P a to je spor, protože cesta P byla v grafu G maximální. Platí původní tvrzení. ■

Z tvrzení ⇒ všichni sousedé vrcholu v1 se nachází na cestě P.

Vrchol v1 má minimálně k sousedů ∧ tvrzení ⇒ cesta P má minimálně k + 1 vrcholů (vrchol v1 a k sousedů vrcholu v1) ⇒ délka cesty P = (v1,v2,...,vi,...,vk+1,...,vs) je alespoň k (samozřejmě platí: k+1≤s) ⇒ pak část cesty P spolu s hranou {v1,vk+1} tvoří kružnici délky alespoň k+1: C = (v1,v2,...,vk+1)∪{vk+1,v1} = (v1,v2,...,vk+1,v1) .

23. Dokažte, že každý graf, který má alespoň dva vrcholy, obsahuje dva vrcholy stejného stupně.

Výsledek

Důkaz sporem:

Nechť tvrzení neplatí, pak: Existuje graf G, který má všechny vrcholy různého stupně. Nechť G má n vrcholů, vrcholy označme v0,v1,v2,...,vn-1.

⇒ Vrcholy grafu G nabývají n navzájem různých stupňů: 0,1,2,...,n-1 (pozn. maximální stupeň v grafu, který má n vrcholů je n-1). Můžeme předpokládat, že deg(v0) = 0, deg(v1) = 1,..., deg(vn-1) = n-1 . A to je spor, protože vrchol stupně 0 a stupně n-1 se v grafu, který má n vrcholů, současně vyskytnout nemůžou. (Vrchol stupně n-1 musí sousedit s n-1 vrcholy, ale když se v grafu s n vrcholy vyskytuje i vrchol stupně 0, pak vrchol může sousedit maximálně s n-2 vrcholy.) Proto předpoklad, že existuje graf G, který má všechny vrcholy stupně různého je špatný a platí původní tvrzení.

24. Dokažte, nebo vyvraťte:

když v grafu G existují dva různé u-v sledy, tak G obsahuje kružnici,
když v grafu G existují dvě různé u-v cesty, tak G obsahuje kružnici.

Výsledek

Důkaz (a):

Tvrzení: Když v grafu G existují dva různé u-v sledy, tak G obsahuje kružnici. – neplatí, protože existuje kontrapříklad:

Existují dva různe u-v sledy: S1 = (u,e1,w,e2,v) a S2 = (u,e1,w,e1,u,e1,w,e2,v) a graf G neobsahje kružnici.

Důkaz přímo (b):

Nechť P1 = (u=x1,x2,x3,...,xk=v) a P2 = (u=y1,y2,...,yl=v) jsou dvě různé u-v cesty ⇒ existuje vrchol, v kterém se cesty rozcházejí a pak vrchol, v kterém se cesty scházejí. Pak vezmeme první vrchol, v kterém se cesty rozcházejí a hned vrchol, v kterém se scházejí (můžou to být i vrcholy x a y, nebo některé vnitřní). Nechť první vrchol, v kterém se cesty rozcházejí je xi = yj, i∈{1,2,...,k}, j∈{1,2,...,l} a vrchol, ve kterém se scházejí je xs = yr, s∈{1,2,...,k}, r∈{1,2,...,l}∧s>i∧r>j.Pak podle definice kružnice je (xi,xi+1,...,xs = yr,...,yj = xi) je kružnice.

25. Nechť G je graf. Jestliže e je most v G, pak v G neexistuje kružnice obsahující hranu e. Dokažte sporem.

Výsledek

Důkaz sporem:

Nechť tvrzení neplatí, pak: Hrana e je most v G a současně v G existuje kružnice obsahující hranu e. V G existuje kružnice C obsahující hranu e={x,y} ⇒ v G existují minimálně 2 x-y cesty: Pxy = e = {x,y} (hrana e) a P´xy = C - e = (x,v1,v2,...,vs,y) (kružnice bez hrany e) .

Teď ukážeme pro ∀u,v∈V(G): jestliže ∃uv-cesta Puv v G ⇒ ∃ uv-cesta P´uv v G-e:

když v G uv-cesta Puv neobsahuje hranu e, pak P´uv = Puv,
když v G uv-cesta Puv obsahuje hranu e, pak hranu e v P´uv nahradíme P´xy (x-y cestou po kružnici C), tím vznikne uv-sled v G-e: (Puv - e)∪P´xy = (Puv - e)∪(C - e) ⇒ existuje i uv-cesta v G-e

z toho všeho plyne

⇒ počet komponent G-e je stejný jako počet komponent G ⇒(dle def. mostu)⇒ e není most, což je spor s předpokladem, proto platí původní tvrzení.

26. Nechť G je souvislý graf. Jestliže e není most v G, pak v G existuje kružnice obsahující hranu e. Dokažte přímo.

Výsledek

Důkaz přímo:

e={x,y}není most v G ⇒(dle def. mostu)⇒ G-e má stejný počet komponent jako G a platí: ∀u,v∈V(G):když existuje u-v cesta P v G, tak existuje u-v cesta P´ v G-e (pozn. P´ se nemusí nutně = P) ⇒ ∃x-y cesta Pxy v G-e ⇒ x-y cesta Pxy se nachází i v G (protože G vznikne z G-e přidáním hrany e) ⇒(dle def. kružnice)⇒ x-y cesta Pxy spolu s hranou e={x,y} tvoří kružnici v G obsahující hranu e.

27. Nechť G je graf. Jestliže v G neexistuje kružnice, pak každá hrana v G je most. Dokažte nepřímo.

Výsledek

Důkaz nepřímo:

Dokážeme následující: Jestliže existuje hrana v G, která není most, pak v G existuje kružnice. Toto dokážeme přímo:

Existuje e={x,y}, která není most v G ⇒(dle def. mostu)⇒ G-e má stejný počet komponent jako G a platí: ∀u,v∈V(G): když existuje u-v cesta P v G, tak existuje u-v cesta P´ v G-e (pozn. P´ se nemusí nutně = P) ⇒ ∃ x-y cesta Pxy v G-e ⇒ x-y cesta Pxy se nachází i v G (protože G vznikne z G-e přidáním hrany e) ⇒(dle def. kružnice)⇒ x-y cesta Pxy spolu s hranou e tvoří kružnici v G.

28. Nechť G je graf. Jestliže každá hrana v G je most, pak v G neexistuje kružnice. Dokažte sporem.

Výsledek

Důkaz sporem:

Nechť tvrzení neplatí, pak: Nechť každá hrana v G je most a současně v G existuje kružnice.

V G existuje kružnice C, nechť e={x,y} je její libovolná hrana ⇒ v G existují minimálně 2 x-y cesty: Pxy = e = {x,y} (hrana e) a P´xy = C-e = (x,v1,v2,...,vs,y) (kružnice bez hrany e) .

Teď ukážeme pro ∀u,v∈V(G): jestliže ∃uv - cesta Puv v G ⇒ ∃uv - cesta P´uv v G-e:

když v G uv-cesta Puv neobsahuje hranu e, pak P´uv = Puv,
když v G uv-cesta Puv obsahuje hranu e, pak hranu e v P´uv nahradíme P´xy (x-y cestou po kružnici C), tím vznikne uv-sled v G-e: (Puv-e)∪P´xy=(Puv-e)∪(C-e) ⇒ existuje i uv-cesta v G-e

⇒ počet komponent G-e je stejný jako počet komponent G ⇒(dle def. mostu)⇒ existuje hrana e, která není most a to je spor s předpokladem. Teda platí původní tvrzení.

29. Dokažte, že když dvě různé kružnice grafu G obsahují hranu e, pak v G existuje i kružnice neobsahující hranu e.

Výsledek

Důkaz přímo:

Nechť e={u,v} a C1=(u=x1,x2,x3,...,xk=v,u) a C2=(u=y1,y2,...,yl,=v,u) jsou dvě různé kružnice, které obsahují hranu e. Můžou nastat dvě možnosti:

C1∩C2 = {e} (tj. kružnice mají společnou jenom hranu e) ⇒(dle def. kružnice)⇒ (u,x2,...,xk=v=yl,yl-1,...,y2,y1=u) je kružnice neobsahující hranu e,
C1∩C2 = {e,e1,...}(tj. kružnice mají kromě hrany e ještě jiné společné hrany), pak máme dvě různé u-v cesty P1 = C1-e = (u=x1,x2,x3,...,xk=v) a P2 = C2-e = (u=y1,y2,y3,...,yl=v) a žádna z cest neobsahuje hranu e ⇒

⇒ existuje vrchol, v kterým se cesty rozcházejí a pak vrchol, v kterém se cesty scházejí. Pak vezmeme první vrchol, v kterém se cesty rozcházejí a hned vrchol, v kterém se scházejí (můžou to být i vrcholy x a y, nebo některé vnitřní). Nechť první vrchol, v kterém se cesty rozcházejí je xi=yj, i∈{1,2,...,k}, j∈{1,2,...,l} a vrchol, v kterém se scházejí je xs=yr, s∈{1,2,...,k}, r∈{1,2,...,l}∧s>i∧r>j.Pak podle definice kružnice je (xi,xi+1,...,xs = yr,...,yj = xi) je kružnice neobsahující hranu e, protože ani jedna z cest jí neobsahovala.

Zdroje textů

DIMA - diskrétní matematika, http://oliva.uhk.cz
Hliněný, Petr. Diskrétní Matematika (456-533 DIM), 2006
Kovář, Petr. DISKRÉTNÍ MATEMATIKA a ÚVOD DO TEORIE GRAFŮ ( příklady k procvičení ), 2012

DIMA - Teorie grafů

Základní terminologie

Obsah ⇫

Teorie ⇫

Definice grafu:

Definice - koncové vrcholy, incidentnost, sousednost:

Definice podgrafu – faktorový, indukovaný:

Definice stupně vrcholu:

Definice – multigraf, pseudograf:

Definice kompletního (úplného) grafu

Definice bipartitního grafu

Definice regulárního grafu

Definice odebrání vrcholu

Definice odebrání hrany

Definice sledu:

Definice tahu:

Definice cesty:

Definice kružnice:

Definice souvislosti:

Definice komponenty:

Definice artikulace/mostu:

Definice vzdálenosti:

Definice izomorfismu:

Definice matice sousednosti:

Seznam sousedních vrcholů

Věta:

Definice incidenční matice:

Definice doplňku (=komplementu):

Definice grafové posloupnosti:

Veta o grafové posloupnosti (o skóre grafu):

Řešený příklad ⇫

Úlohy k řešení ⇫

Zdroje textů