Problém minimální kostry
Obsah ⇫
- minimální kostra grafu
- Borůvkův algoritmus nalezení minimální kostry
- Jarníkův (Primův) algoritmus nalezení minimální kostry
- Kruskalův algoritmus nalezení minimální kostry
Teorie ⇫
Problém určení minimální kostry je motivován mnoha praktickými aplikacemi v reálném životě (hledání nejkratšího vlakového spoje, hledání nejlevnějšího propojení kabely…). Problém určení minimální kostry má také svoji historii , do které se zapsali i dva čeští matematici. Nejprve je formuloval a úspěšně vyřešil v polovině 20. let O. Borůvka na zakázku společnosti MEZ v souvislosti s návrhem sítě pro rozvod elektřiny na Moravě. Efektivnější metodu řešení navrhnul v roce 1930 V. Jarník.
Řešení problému minimální kostry grafu byla v obou podobách (Borůvky a Jarníka) nezávisle znovuobjevena ještě několikrát. Jedním z důvodů "znovuobjevování" byla jistě skutečnost, že většina prací byla psána v mateřském jazyku autora a často tak matematikům z jiných zemí nedostupná. To je i případ Primova algoritmu, který je vlastně jen znovuobjevený Jarníkův algoritmus.
Třetí řešení, odlišné od předchozích dvou, podal roku 1956 Joseph B. Kruskal ve své práci On the shortest spanning tree of a graph and the traveling salesman problem.
Definice problému:
Nechť je dán souvislý graf G=(V,E). Nechť pro každou hranu e grafu G je dáno reálné číslo w(e), tzv. ohodnocení hrany e. Mezi všemi kostrami grafu G najděte kostru H=(V,E'), pro kterou součet ohodnocení hran w(H)=∑w(e), kde e∈E', nabývá minimální hodnoty. Kostru H nazveme minimální kostrou grafu G a w(H) cenou kostry H.
V definici se uvažuje ohodnocení hran reálným číslem. V praxi se vesměs jedná o čísla nezáporná.
Nezřídka se setkáme i s úlohou nalezení minimální kostry v grafu, ve kterém je nutné některá spojení vyloučit (tzv. zakázané hrany) a jiná se naopak musí ve výsledném řešení nacházet (tzv. povinné hrany). V takovém případě provedeme jednoduchou úpravu ohodnocení hran v daném grafu. Hranám povinným přiřadíme ohodnocení menší než je ohodnocení ostatních hran a hrany zakázané z grafu odebereme. Pokud by se jednalo o hrany nejméně vhodné, nikoli zakázané, přiřadíme jim ohodnocení větší než jaké mají ostatní hrany.
Minimálních koster v daném grafu může být více. Stačí si představit krajní případ, graf, jehož všechny hrany jsou ohodnoceny stejným číslem. V takovém grafu je zřejmě počet minimálních koster roven počtu všech koster.
Více informací o historii problému lze najít v monografii Problém minimální kostry grafu, která se celou touto problematikou zabývá detailně. Zájemci ji mají k dispozici na BlackBoardu.
Tři klasická řešení problému minimální kostry
Pomocí procesu barvení hran popíšeme Borůvkovo, Jarníkovo a Kruskalovo řešení, přičemž počet vrcholů značíme n a počet hran m. U Borůvkova algoritmu předpokládáme, že žádné dvě hrany nemají stejné ohodnocení (což lze předpokládat bez újmy na obecnosti).
Borůvkův algoritmus
Na počátku nechť je každá hrana grafu G neobarvená a nechť každý vrchol grafu G představuje modrý strom (uvažujeme modrý les složený z n modrých stromů).
V každém kroku algoritmu, dokud modré hrany netvoří strom, provádíme:
- pro každý modrý strom najdeme mezi všemi hranami, jejichž jeden vrchol leží v uvažovaném stromu a druhý nikoli, hranu s nejmenším ohodnocením. Tyto hrany obarvíme modře (získáme nový modrý les).
Algoritmus končí získáním modrého stromu - minimální kostry grafu G.
Algoritmus
Vstup: Graf G s ohodnocením w
K1: T = (V(G),∅)
K2: Dokud T má alespoň dvě komponenty opakuj:
- Pro každou komponentu Ti vybereme nejlehčí incidentní hranu ti
- Všechny hrany ti přidáme do T
Výstup: Minimální kostra T
Jarníkův algoritmus (v zahraničí známý jako Primův)
Na počátku nechť je každá hrana grafu G neobarvená. Zvolíme libovolný vrchol a považujeme jej za modrý strom.
V každém z (n-1) kroků obarvíme modře hranu s minimálním ohodnocením, jejíž jeden vrchol leží v modrém stromu a druhý v něm neleží (existuje-li jich více, zvolíme k obarvení libovolnou z nich).
Algoritmus končí získáním modrého stromu - minimální kostry grafu G.
Algoritmus
Vstup: souvislý ohodnocený graf G(V,E)
K1: Inicializace: V' = {x}, kde x je libovolný vrchol z V,E' = {}
K2: Dokud není V'=V opakuj:
- Vyber hranu (u,v) z E s minimální cenou tak, že u je ve V' a v není ve V'
- Přidej v do V', přidej (u,v) do E'
Výstup: T(V',E') je minimální kostra grafu
Kruskalův algoritmus
Na počátku nechť je každá hrana grafu G neobarvená. Provedeme uspořádání hran neklesajícím způsobem dle jejich ohodnocení. Každý vrchol grafu G považujeme za modrý strom.
V každém z m kroků rozhodneme o právě jedné hraně (v pořadí daném jejich uspořádáním), zda ji obarvíme modře či nikoli. Modře hranu obarvíme právě tehdy, když netvoří s modře obarvenými hranami kružnici (tj. když koncové vrcholy hrany neleží v témž modrém stromu).
Algoritmus ukončíme, jakmile je (n-1) hran obarveno modře. Tyto modré hrany tvoří minimální kostru grafu G.
Algoritmus
Vstup: Graf G s ohodnocením w
K1: Setřídíme všechny hrany z E(G) tak, aby: w(e1) < ... < w(em)
K2: T = (V (G), ∅)
K3: Pro i=1 do m opakuj
- pokud T∪ei je acyklický, provedeme T = T∪ei (jestliže koncové vrcholy hrany ei leží v různých komponentách, sjednotíme obě tyto komponenty)
Výstup: Minimální kostra T
Základní rozdíl mezi uvedenými řešeními lze charakterizovat následovně:
- Kruskalův algoritmus v každém kroku, ve kterém dojde k obarvení hrany modře, spojuje navzájem dva nejbližší modré stromy v jeden modrý strom.
- Jarníkův algoritmus v každém kroku rozšiřuje stále jediný modrý strom, obsahující počáteční vrchol, o nejbližší vrchol.
- V Borůvkově algoritmu dochází v každém kroku ke spojení všech navzájem si nejbližších modrých stromů.
Ilustrace algoritmů
Ilustrace jednotlivých algoritmů na zadaném grafu jsou představeny v monografii Problém minimální kostry grafu [Milková, E.: Problém minimální kostry grafu, Gaudeamus, Hradec Králové, 2001], zde je ilustrujeme na grafu zadaném maticí sousednosti – viz níže.
| a | b | c | d | e | f | g | h | i | j | k | |
| a | 1 | 7 | 22 | ||||||||
| b | 1 | 2 | |||||||||
| c | 7 | 2 | 30 | ||||||||
| d | 22 | 11 | 16 | ||||||||
| e | 31 | 6 | |||||||||
| f | 30 | 11 | 31 | 18 | 35 | 28 | |||||
| g | 16 | 6 | 18 | ||||||||
| h | 35 | 8 | 24 | ||||||||
| i | 8 | 13 | |||||||||
| j | 24 | 13 | 5 | ||||||||
| k | 28 | 5 |
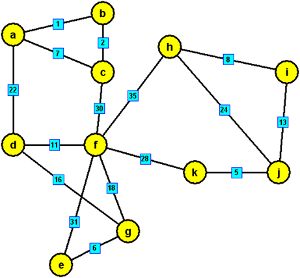
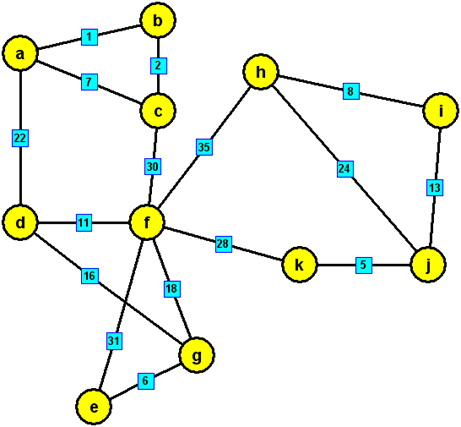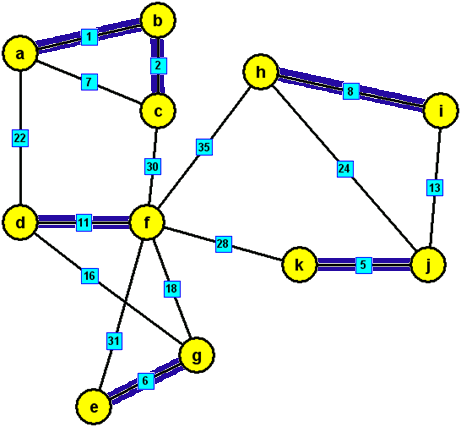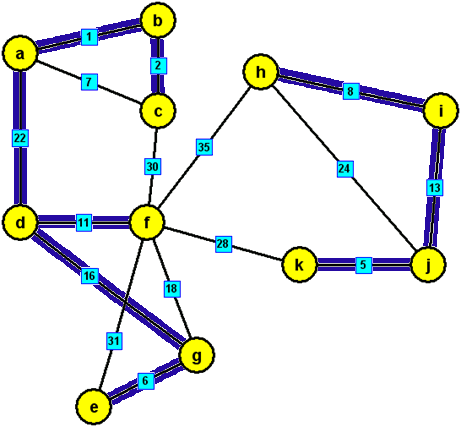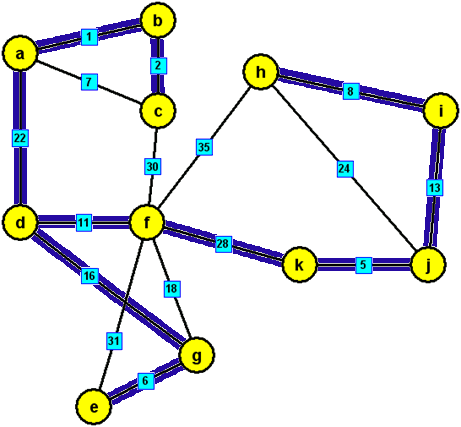
Borůvkův algoritmus
V prvním kroku si vypíšeme ke každému vrcholu nejméně ohodnocenou hranu a vytvoříme les stromů obsahujících všechny vrcholy. V každém dalším kroku tyto stromy rozšiřujeme o další nejméně ohodnocené hrany s těmito stromy incudentními.
| 1. krok | les | 2. krok | les | 3. krok | les |
| a b 1 | {a,b,c} | a d 22 | {a,b,c,d,f,e,g} | f k 28 | {a,b,c,d,f,e,g,h,i,j,k} |
| b a 1 | {d,f} | d g 16 | {h,i,j,k} | k f 28 | |
| c b 2 | {e,g} | g d 16 | |||
| d f 11 | {h,i} | i j 13 | |||
| e g 6 | {j,k} | j i 13 | |||
| f d 11 | |||||
| g e 6 | |||||
| h i 8 | |||||
| i h 8 | |||||
| j k 5 | |||||
| k j 5 |
modré hrany, které tvoří minimální kostru zadaného grafu: {a,b},{c,b},{d,f},{e,g},{h,i},{j,k},{a,d},{d,g},{i,j}, {f,k}
Jarníkův algoritmus
Tady rozšiřujeme modrý strom vždy o nejméně ohodnocenou incidentní hranu.
| a | b | c | d | e | f | g | h | i | j | k | |
| a | 1 | 7 | 22 | ||||||||
| b | 1 | 2 | |||||||||
| c | 7 | 2 | 30 | ||||||||
| d | 22 | 11 | 16 | ||||||||
| e | 31 | 6 | |||||||||
| f | 30 | 11 | 31 | 18 | 35 | 28 | |||||
| g | 16 | 6 | 18 | ||||||||
| h | 35 | 8 | 24 | ||||||||
| i | 8 | 13 | |||||||||
| j | 24 | 13 | 5 | ||||||||
| k | 28 | 5 |
| a | (0,a) | |||||||||
| b | (1,a) | |||||||||
| c | (7,a) | (2,b) | ||||||||
| d | (22,a) | (22,a) | (22,a) | |||||||
| e | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (31,f) | (6,g) | ||||
| f | (∞,a) | (∞,a) | (30,c) | (11,d) | ||||||
| g | (∞,a) | (∞,a) | (∞,a) | (16,d) | (16,d) | |||||
| h | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (35,f) | (35,f) | (35,f) | (35,f) | (24,j) | (8,i) |
| i | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (13,j) | |
| j | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (5,k) | ||
| k | (∞,a) | (∞,a) | (∞,a) | (∞,a) | (28,f) | (28,f) | (28,f) |
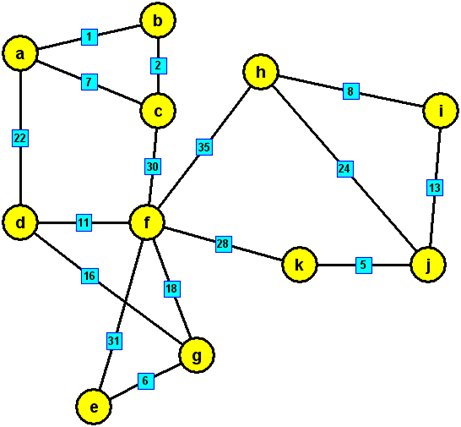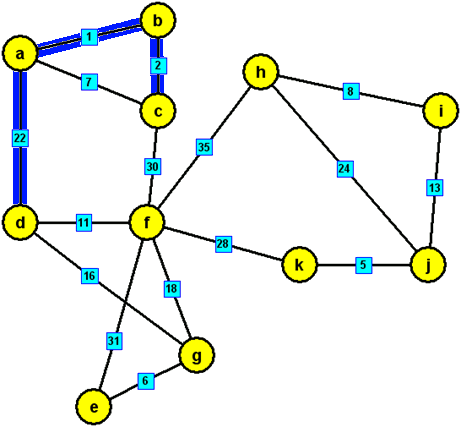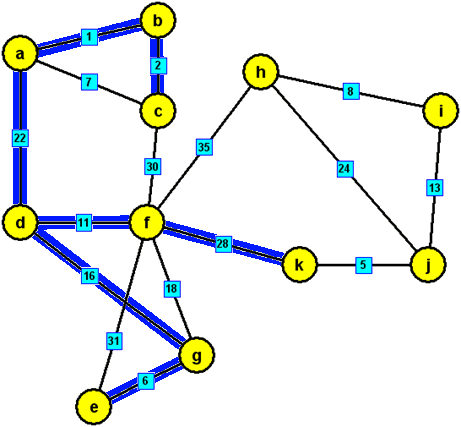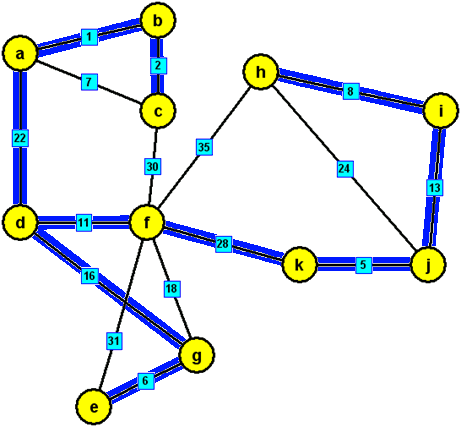
modré hrany, které tvoří minimální kostru zadaného grafu: {a,b},{b,c},{a,d},{g,e},{d,f},{d,g},{i,h},{j,i}, {k,j},{f,k}
Kruskalův algoritmus
Zde si sestavíme seznam hran od nejméně ohodnocené po nejvíce. V seznamu vrcholů postupně rozšiřujeme stromy, až nám vznikne jediný.
| hrana | les | obarvi modře |
| {a} {b} {c} {d} {e} {f} {g} {h} {i} {j} {k} | ||
| {a,b} | {a} {b} {c} {d} {e} {f} {g} {h} {i} {j} {k} | ANO |
| {b,c} | {a, b} {c} {d} {e} {f} {g} {h} {i} {j} {k} | ANO |
| {k,j} | {a, b, c} {d} {e} {f} {g} {h} {i} {j} {k} | ANO |
| {e,g} | {a, b, c} {d} {e} {f} {g} {h} {i} {j, k} | ANO |
| {a,c} | {a, b, c} {d} {e, g} {f} {h} {i} {j, k} | NE |
| {h,i} | {a, b, c} {d} {e, g} {f} {h} {i} {j, k} | ANO |
| {d,f} | {a, b, c} {d} {e, g} {f} {h, i} {j, k} | ANO |
| {i,j} | {a, b, c} {d, f} {e, g} {h, i} {j, k} | ANO |
| {d,g} | {a, b, c} {d, f} {e, g} {h, i, j, k} | ANO |
| {f,g} | {a, b, c} {d, f, e, g} {h, i, j, k} | NE |
| {a,d} | {a, b, c} {d, f, e, g} {h, i, j, k} | ANO |
| {h,j} | {a, b, c, d, f, e, g} {h, i, j, k} | NE |
| {f,k} | {a, b, c, d, f, e, g} {h, i, j, k} | ANO |
| {c,f} | {a, b, c, d, f, e, g, h, i, j, k} | NE |
| {e,f} | {a, b, c, d, f, e, g, h, i, j, k} | NE |
| {f,h} | {a, b, c, d, f, e, g, h, i, j, k} | NE |
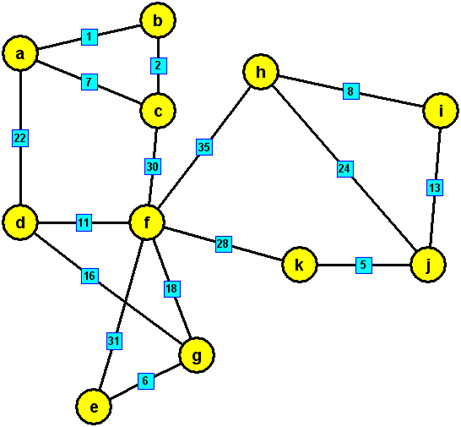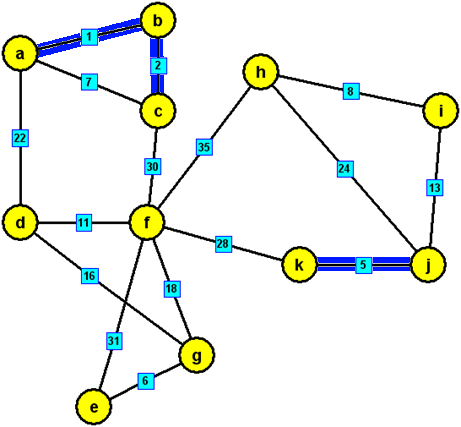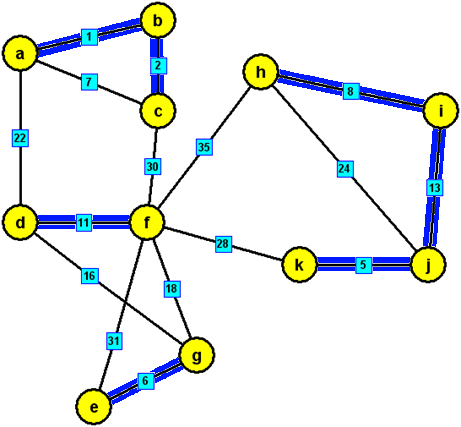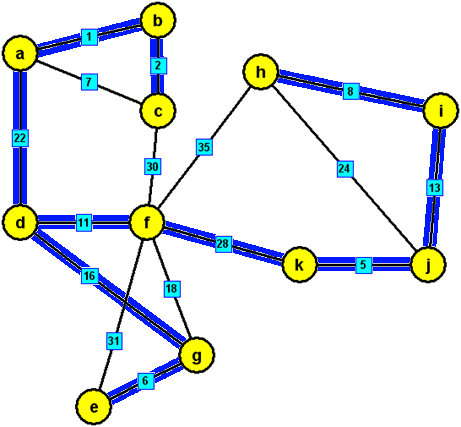
modré hrany, které tvoří minimální kostru zadaného grafu: {a,b},{b,c},{k,j},{e,g},{h,i},{d,f},{i,j},{d,g},{a,d},{f,k}
Pozn.: Vzhledem k tomu, že ohodnocení hran daného grafu je navzájem různé, dostali jsme ve všech třech případech stejnou minimální kostru grafu.
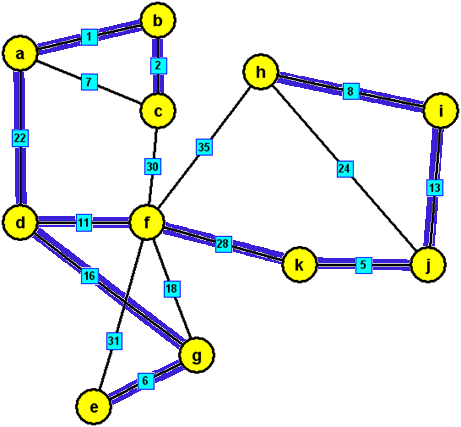
Příklad
V následujícím grafu zadaném maticí cen určete Kruskalovým algoritmem minimální kostru a její cenu. Graf nekreslete!
| A | B | C | D | E | F | G | H | |
| A | 1 | 1 | 3 | |||||
| B | 1 | 4 | 1 | |||||
| C | 1 | 4 | 1 | 4 | ||||
| D | 3 | 1 | 1 | 1 | 5 | |||
| E | 4 | 1 | ||||||
| F | 1 | 0 | 2 | |||||
| G | 5 | 0 | ||||||
| H | 1 | 2 |
Nejprve si vypíšeme všechny hrany pod sebe od nejmenší po největší. Vedle hran si vypíšeme vrcholy. Do třetího sloupce budeme zapisovat, zda hranu použijeme v kostře či nikoli.
| FG | {A}{B}{C}{D}{E}{FG}{H} | ano |
| AB | {AB}{C}{D}{E}{FG}{H} | ano |
| AC | {ABC}{D}{E}{FG}{H} | ano |
| BH | {ABCH}{D}{E}{FG} | ano |
| CD | {ABCHD}{E}{FG} | ano |
| DE | {ABCHDE}{FG} | ano |
| DF | {ABCHDEFG} | ano |
| FH | {ABCHDEFG} | ne |
| AD | {ABCHDEFG} | ne |
| BC | {ABCHDEFG} | ne |
| CE | {ABCHDEFG} | ne |
| DG | {ABCHDEFG} | ne |
Minimální kostra je tvořena hranami u kterých máme ano. (FG=0,AB=1,AC=1,BH=1,CD=1,DE=1,DF=1)
Po sečtení ohodnocení hran dostaneme cenu kostry - tedy číslo 6.
Řešený příklad ⇫
1. Jistá televizní společnost potřebuje položit v dané lokalitě kabely, aby propojila vybrané domácnosti. Možnosti propojení a vzdálenosti mezi jednotlivými domácnostmi jsou uvedeny na následujícím grafu. Zjistěte, kde by televizní společnost měla kabely položit, aby co nejlevnějším způsobem propojila všechny domácnosti (tj. aby spotřeba kabelů byla co nejmenší).
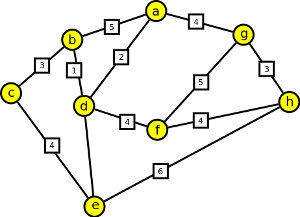
Krok 1
Použijeme např. Borůvkův algoritmus. Vybereme ke každému vrcholu hranu s nejmenším ohodnocením a vytvoříme les obsahující všechny vrcholy:
| 1. tah | |
| ad | |
| bd | |
| cb | |
| ec | |
| fd | |
| gh |
Tím nám vznikne les se stromy: {a,b,c,d,e,f} a {g,h}.
Krok 2
Vybereme nejméně ohodnocenou hranu spojující oba stromy. Je to např. hrana ag.
| 2. tah |
| ag |
Krok 3
Tím dostaneme výslednou min. kostru obsahující hrany: ad,bd,cb,ec,fd,ag,gh můžeme prohlásit:
Aby spotřeba kabelů byla co nejmenší, musí televizní společnost položit kabely mezi městy ab, bd, cb, ec, fd, ag a gh.
Úlohy k řešení ⇫
1. Policie velkoměsta v Americe se rozhodla, že mezi svými stanicemi vytvoří propojení informačních systémů za pomoci optických kabelů. Propojeny musí být všechny stanice. Jakou délku kabelů musejí použít?
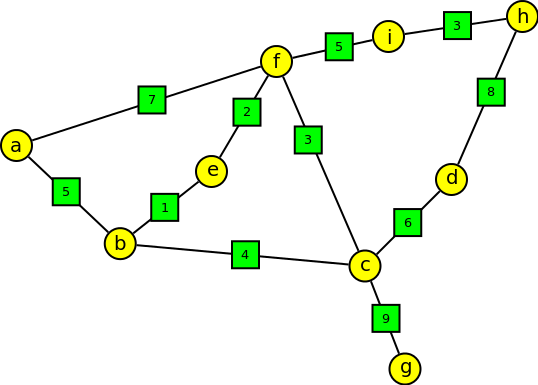
Výsledek
34
2. V jedné oblasti byli malé vesničky propojené, jenom kamennými cestičkami. Po takových kamenných cestách se autem nejezdí moc pohodlně, a tak se obyvatelé rozhodli, že některé cesty vyasfaltují. Nemusí existovat vyasfaltovaná cesta přímo mezi každými 2 vesničkami, ale chtějí, aby existovalo spojení po asfaltové cestě mezi každými 2 vesničkami. Poradíte jim, které cestičky vyasfaltovat, aby použili co nejméně asfaltu? Napište postupně hrany, jak je přidáváte do kostry pomocí Jarníkova algoritmu.
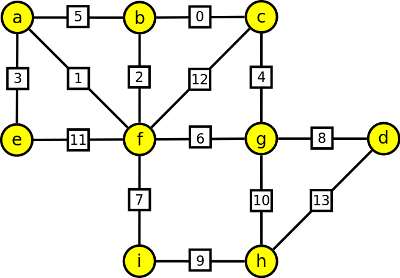
Výsledek
Hrany: af,fb,bc,ae,cg,fi,gd,ih. Cena: 34.
3. V následujícím grafu zadaném maticí určete Kruskalovým algoritmem minimální kostru. Vypište množinu jejich hran a cenu. Graf nekreslete.
| A | B | C | D | E | F | G | H | |
| A | 1 | 1 | 3 | |||||
| B | 1 | 4 | 1 | |||||
| C | 1 | 4 | 1 | 4 | ||||
| D | 3 | 1 | 1 | 1 | 5 | |||
| E | 4 | 1 | ||||||
| F | 1 | 0 | 2 | |||||
| G | 5 | 0 | ||||||
| H | 1 | 2 |
Výsledek
Hrany: FG,AB,AC,BH,CD,DE,DF. Cena: 6.
4. Najděte minimální kostru grafu pomocí Borůvky, Jarníka a Kruskala a napiště ohodnoceníé minimální kostry. (Popište postup: pořadí hran, které zadáváte do kostry.)
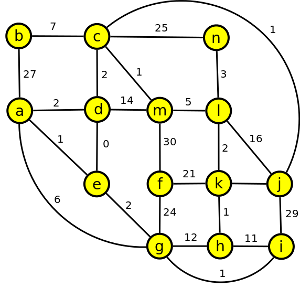
Zdroje textů
- DIMA - diskrétní matematika, http://oliva.uhk.cz
- Milková, E.. Problém minimální kostry grafu, Hradec Králové: Gaudeamus, 2001
- Hliněný, Petr. Diskrétní Matematika (456-533 DIM), 2006
- Kovář, Petr. DISKRÉTNÍ MATEMATIKA a ÚVOD DO TEORIE GRAFŮ ( příklady k procvičení ), 2012