Prohledávání grafu
Obsah ⇫
- prohledávání grafu do hloubky
- prohledávání grafu do šířky
- algoritmus prohledávání do šířky
- algoritmus prohledávání do hloubky
- určení souvislostí grafu
- určení počtu komponent
- určení, zda daná hrana je most
- určení, zda dva vrcholy spolu souvisí (zda se nachází v jedné komponentě souvislosti)
- určení vzdáleností a minimální cesty mezi danými vrcholy x,y
- určení, zda graf je bipartitní
- určení, zda existuje kružnice obsahující daný vrchol
- určení, zda existuje kružnice obsahující danou hranu
Teorie ⇫
V praxi často řešíme úlohy, ve kterých objekty reprezentované vrcholy grafu potřebujeme systematicky zpracovat. K těm nejznámějším algoritmům, které provádí systematický průchod všemi vrcholy (systematické zpracování všech vrcholů) daného grafu, patří dva, algoritmus prohledávání do hloubky a algoritmus prohledávání do šířky.
Oba uvedené algoritmy prohledávání vrcholů můžeme pro souvislý graf formulovat velmi jednoduše jako modifikaci Jarníkova algoritmu. Vzpomeňme, že v každém kroku Jarníkova algoritmu zvětšujeme modrý strom o právě jedinou hranu a právě jediný vrchol. Toto postupné zařazování vrcholů do modrého stromu můžeme vnímat jako systematické zpracování jednotlivých vrcholů grafu, ovšem v pořadí, které je závislé na ohodnocení hran grafu. Představme si nyní činnost Jarníkova algoritmu na grafu, jehož všechny hrany jsou ohodnoceny stejným číslem, např. jedničkou. V tom případě je to totéž, jako kdybychom pracovali s grafem neohodnoceným, přičemž v každém kroku můžeme volit z hran, které se dotýkají modrého stromu (tj. z hran, které mají jeden vrchol v modrém stromu a druhý vně tohoto stromu), libovolnou pro zařazení do tohoto stromu. Abychom výběr hrany (a tím i vrcholu), o kterou modrý strom rozšiřujeme, upřesnili, stanovíme pravidla. A ta nám již určují algoritmus prohledávání do hloubky a algoritmus prohledávání do šířky.
Pravidlo H - prohledávání do hloubky
Modrý strom zvětšíme v každém kroku o hranu, která se jej dotýká ve vrcholu, který byl zařazen do modrého stromu jako poslední ze všech, které jsou v daném kroku koncovými vrcholy hran dotýkajících se modrého stromu.
Pravidlo S - prohledávání do šířky
Modrý strom zvětšíme v každém kroku o hranu, která se jej dotýká ve vrcholu, který byl zařazen do modrého stromu jako první ze všech, které jsou v daném kroku koncovými vrcholy hran dotýkajících se modrého stromu.
Proč právě názvy „prohledávání do hloubky“ a „prohledávání do šířky“?
Představme si, že uvedené algoritmy aplikujeme na kořenový strom. Je zřejmé, že při použití pravidla H zařazujeme vrcholy do modrého stromu v kořenovém stromu ve směru „dolů“, do hloubky, a při použití pravidla S zařazujeme vrcholy do modrého stromu „po vrstvách“ kořenového stromu, tj. pohybujeme se do šířky.
Pozn.: Na grafech, které nejsou souvislé, budeme zcela přirozeně postupně prohledávat jednotlivé komponenty daného grafu.
Vztah algoritmů prohledávání s Jarníkovým přístupem k hledání minimální kostry grafu jsme uvedli záměrně, aby bylo zřejmé, že při algoritmech prohledávání vytváříme (modrou) kostru grafu. Tu když znázorníme jako kořenový strom s kořenem ve vrcholu, ve kterém začínáme prohledávání, dostáváme zajímavé výsledky. Ilustrujme je na následujícím grafu.
Ještě poznamenejme, že k tomu, abychom jednoduše určili vrchol, z kterého provedeme rozšíření modrého stromu při použití pravidla H, využijeme datovou strukturu zásobník (LIFO) a k tomu, abychom jednoduše určili vrchol, z kterého provedeme rozšíření modrého stromu při použití pravidla S, využijeme datovou strukturu frontu (FIFO).
Algoritmus prohledávání do hloubky
Nechť je dán souvislý graf G = (V,E) s n vrcholy a m hranami a nechť vrchol v je libovolný vrchol množiny V. Úkolem je systematicky zpracovat všechny vrcholy a hrany grafu G.
začátek
na počátku nechť je graf G neobarvený. Zpracuj vrchol v, obarvi jej modře (považujeme jej za modrý strom) a vlož do zásobníku LIFO.
dokud není zásobník LIFO prázdný opakuj
začátek
x : = vrchol ležící na posledním místě v zásobníku LIFO;
jestliže x je koncovým vrcholem neobarvené hrany {x,y} pak
začátek
jestliže hrana {x,y} se dotýká modrého stromu (tj. y je neobarvený) pak
začátek
zpracuj vrchol y, obarvi jej modře a vlož do zásobníku LIFO;
zpracuj hranu {x,y} a obarvi ji modře;
konec
jinak (tj. vrchol y je již obarven modře)
zpracuj hranu {x,y} a obarvi ji červeně;
konec
jinak (tj. x není koncovým vrcholem žádné neobarvené hrany)
odeber x ze zásobníku LIFO;
konec;
konec.
Ilustrace algoritmu prohledávání vrcholů souvislého grafu do hloubky:
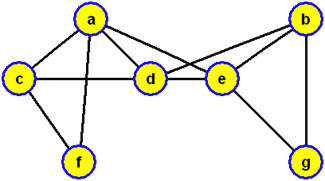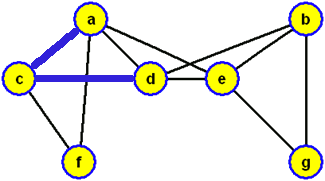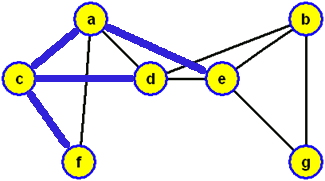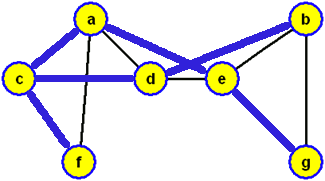
Začneme-li na následujícím grafu
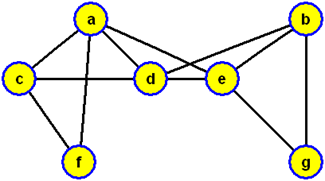
prohledávání vrcholů do hloubky ve vrcholu c a použijeme-li při výběru hrany zařazované do modrého stromu lexikografické pravidlo (tj. pokud existuje více hran {x,y}, které se dotýkají modrého stromu ve vrcholu x, volíme vrchol y vzhledem k abecednímu pořadí koncových vrcholů těchto hran), budou vrcholy zpracovány v pořadí c, a, d, b, e, g, f, přičemž bude konstruována modrá kostra grafu
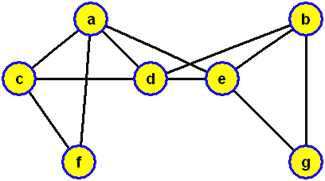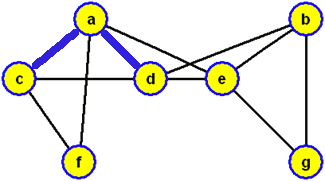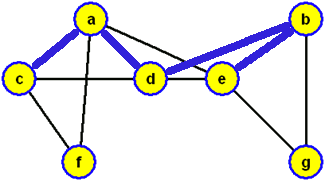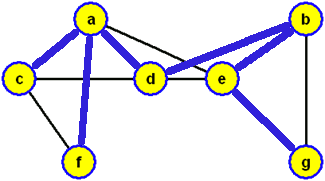
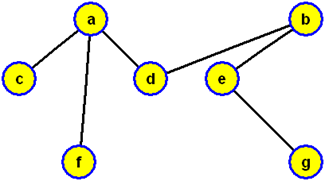
a když ji zobrazíme jako kořenový strom s kořenem c, dostaneme strom prohledávání do hloubky (příslušný právě provedenému algoritmu prohledávání do hloubky s počátkem prohledávání ve vrcholu c)
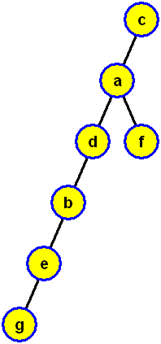
Algoritmus prohledávání do šířky
Nechť je dán souvislý graf G = (V,E) s n vrcholy a m hranami a nechť vrchol v je libovolný vrchol množiny V. Úkolem je systematicky zpracovat všechny vrcholy a hrany grafu G.
začátek
na počátku nechť je graf G neobarvený.
Zpracuj vrchol v, obarvi jej modře (považujeme jej za modrý strom)a vlož do fronty FIFO.
dokud není fronta FIFO prázdná opakuj
začátek
x : = vrchol ležící na prvním místě ve frontě FIFO;
jestliže x je koncovým vrcholem neobarvené hrany {x,y} pak
začátek
jestliže hrana {x,y} se dotýká modrého stromu (y-neobarvený) pak
začátek
zpracuj vrchol y, obarvi jej modře a vlož do fronty FIFO;
zpracuj hranu {x,y} a obarvi ji modře;
konec
jinak (tj. vrchol y je již obarven modře)
zpracuj hranu {x,y} a obarvi ji červeně;
konec
jinak (tj. x není koncovým vrcholem žádné neobarvené hrany)
odeber x z fronty FIFO;
konec;
konec.
Ilustrace algoritmu prohledávání vrcholů souvislého grafu do šířky:
Začneme-li, na stejném grafu jako výše, prohledávání do šířky ve vrcholu c a respektujeme-li již zmíněné lexikografické pravidlo, budou vrcholy zpracovány v pořadí c, a, d, f, e, b, g, přičemž bude konstruována modrá kostra grafu
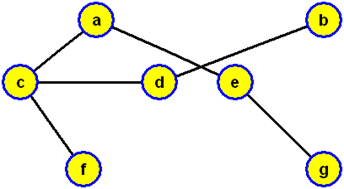
a když ji zobrazíme jako kořenový strom s kořenem c, dostaneme strom prohledávání do šířky (příslušný právě provedenému algoritmu prohledávání do šířky s počátkem prohledávání ve vrcholu c)
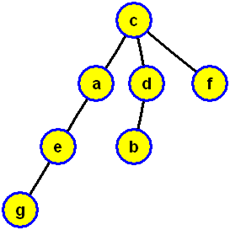
Z uvedených ilustrací je patrné, že pro tentýž graf jsme dostali při prohledávání do hloubky jiný strom prohledávání než ten, který vznikl v průběhu prohledávání do šířky. Oba stromy prohledávání mají, vzhledem k hranám do nich nezařazených, své specifické vlastnosti.
Vlastnost stromů prohledávání do hloubky
- Tvrzení 1:
Nechť G=(V,E) je souvislý graf, TH je modrá kostra získaná algoritmem prohledávání vrcholů grafu G do hloubky se začátkem prohledávání ve vrcholu v a (TH,v) je příslušný strom prohledávání do hloubky. Pak pro koncové vrcholy libovolné neobarvené hrany grafu G platí, že jeden je následníkem druhého ve stromu (TH,v).
- Důkaz:
Nechť {x,y} je libovolná neobarvená hrana grafu G a předpokládejme, že vrchol y byl zařazen do zásobníku (do kostry TH) později než vrchol x (v opačném případě bychom postupovali analogicky). Vzhledem k tomu, že vrchol y je sousedním vrcholem vrcholu x, musel být do zásobníku vložen dříve, než byl vrchol x ze zásobníku odebrán. Odtud plyne, že y leží v podstromu (T´,x) stromu (TH,v) a tudíž je následníkem vrcholu x.∎
Vlastnost stromů prohledávání do šířky
- Tvrzení 2:
Nechť G=(V,E) je souvislý graf, TS je modrá kostra získaná algoritmem prohledávání vrcholů grafu G do šířky se začátkem prohledávání ve vrcholu v a (TS,v) je příslušný strom prohledávání do šířky. Pak pro koncové vrcholy libovolné neobarvené hrany grafu G platí, že tyto vrcholy leží ve stejné vrstvě nebo sousedních vrstvách stromu (TS,v).
Pozn.: sousedními vrstvami stromu (TS,v) máme na mysli i-tou a (i+1)-ní vrstvu, i∈{0, 1, ..., h -1}, kde h je hloubka stromu (TS,v).
- Důkaz:
Nechť {x,y} je libovolná neobarvená hrana grafu G a předpokládejme, že vrchol y byl zařazen do fronty (do kostry TS) později než vrchol x (v opačném případě bychom postupovali analogicky). Nechť x leží ve vrstvě i, i∈{0, 1, ..., h -1}, stromu (TS,v).
Je zřejmě, že vrcholy zařazené do TS později než vrchol x leží ve vrstvě j, kde j≥i, a vrcholy zařazené do TS dříve než byl vrchol x odebrán z fronty leží zřejmě ve vrstvě j, kde j≤i+1. Dle předpokladu a protože vrchol y je sousedním vrcholem vrcholu x v grafu G, platí pro něj oba uvedené vztahy, tj. i≤j≤i+1, což znamená, že vrchol y leží v i-té nebo (i+1)-ní vrstvě.∎
Na základě uvedených vlastností stromů prohledávání formulujme následující tvrzení.
- Tvrzení 3:
Nechť G=(V,E) je souvislý graf, nechť TH je modrá kostra získaná algoritmem prohledávání vrcholů grafu G do hloubky se začátkem prohledávání ve vrcholu v a (TH,v) příslušný strom prohledávání do hloubky. Pak:
- vrchol v je artikulace v grafu G právě tehdy, když vrchol v má alespoň dva přímé následníky ve stromu (TH,v),
- vrchol x≠v je artikulace v grafu G právě tehdy, když ve stromu (TH,v) existuje přímý následník y vrcholu x takový, že ani vrchol y ani jeho následník není spojen v grafu G neobarvenou hranou s předchůdcem vrcholu x.
- Důkaz:
-
⇐Jestliže vrchol v má alespoň dva přímé následníky x1,x2, pak, protože dle tvrzení 1 mezi podstromy (T´,x1) a (T´´,x2) stromu (TH,v) neexistuje neobarvená hrana, tvoří každý z těchto podstromů kostru nějaké komponenty grafu G-v. V grafu G-v tak existují alespoň dvě komponenty, což znamená, že graf G-v není souvislý a tedy vrchol v je artikulace.
⇒dokážeme nepřímo (větu obměněnou). Předpokládáme, že vrchol v má nejvýše jednoho přímého následníka ve stromu (TH,v).
Nemá-li žádného následníka, jedná se o graf obsahující pouze vrchol v, který samozřejmě není artikulace.
Jestliže vrchol v má právě jednoho přímého následníka x, pak zřejmě podstrom (T´,x) stromu (TH,v) tvoří kostru celého grafu G-v, což znamená, že graf G-v je souvislý. Odtud vrchol v není artikulace.
-
⇐Pokud existuje přímý následník y vrcholu x s předpokládanými vlastnostmi, pak opět dle tvrzení 1 podstrom (T´,y) stromu (TH,v) tvoří kostru příslušné komponenty K grafu G-x, kde K≠G-x. Graf G-x není souvislý a tedy vrchol v je artikulace.
⇒dokážeme nepřímo (větu obměněnou). Jestliže neexistuje přímý následník y vrcholu v s předpokládanými vlastnostmi, pak je zřejmé, že každý podstrom (T´,z) stromu (TH,v), kde z je přímý následník vrcholu x, je spojen alespoň jednou neobarvenou hranou s nějakým předchůdcem vrcholu x. Tudíž graf G-x je souvislý a vrchol v není artikulace.∎
-
- Tvrzení 4:
Nechť G je souvislý graf a (TS,v) jeho kořenový strom prohledávání do šířky. Pak délka nejkratší cesty z vrcholu v do vrcholu y v grafu G je rovna h(y), kde h(y) značí číslo vrstvy, ve které leží vrchol y.
Pozn.: Nejkratší cestou z vrcholu x do vrcholu y v hranově neohodnoceném grafu G rozumíme tu cestu mezi těmito vrcholy, která má minimální počet hran.
- Důkaz:
Nechť h(y)=i. Ve stromu (TS,v) a tedy také v grafu G existuje cesta P z kořene v do vrcholu y, která je zřejmě délky i. Podle tvrzení 2 nemůže v grafu G existovat cesta kratší délky.∎
- Tvrzení 5:
Nechť G je souvislý graf a (TS,v) jeho kořenový strom prohledávání do šířky. Pak graf G obsahuje kružnici liché délky právě tehdy, když v grafu G existuje neobarvená hrana s koncovými vrcholy ležícími ve stejné vrstvě stromu (TS,v).
- Důkaz:
⇐Nechť {x,y} je neobarvená hrana v grafu G taková, že h(x)=h(y)=i. Nechť vrchol z je první společný předchůdce vrcholů x,y ve stromu (TS,v), h(z)=j. Takový vrchol zřejmě existuje (přinejmenším vrchol v) a platí j<i. Pak cesta z vrcholu z do vrcholu x spolu s hranou {x,y} a cestou z vrcholu y do vrcholu z tvoří kružnici v grafu G délky (i j)+1+( i j)=2·(i j)+1, což je kružnice liché délky.
⇒dokážeme větu obměněnou. Jestliže v grafu G neexistuje neobarvená hrana s koncovými vrcholy ležícími ve stejné vrstvě stromu (TS,v), pak je snadné ukázat, že graf G je bipartitní. Rozdělme vrcholy grafu G do dvou množin. Do množiny V1 dejme vrcholy k. vrstvy, k=0,2,..., a do množiny V2 vrcholy (k+1). vrstvy. Z předpokladu a z tvrzení 2 plyne, že žádná hrana grafu G nemá oba své koncové vrcholy v téže množině a tudíž graf G je bipartitní. Protože platí věta: Graf G je bipartitní právě tehdy, když v grafu G neexistuje kružnice liché délky, je tímto tvrzení 5 dokázáno.∎
Algoritmy PŠ a PH mají velké využití při zjišťování určitých vlastností grafu:
- Určení, zda graf je souvislý:
- Princip:
- Nechť množina M = V(G). Zvolíme libovolný vrchol z množiny M a spustíme z daného vrcholu prohledávání PŠ nebo PH. Každý vrchol, který bude zpracován při prohledávání, odstraníme z množiny M. Po skončení algoritmu se podíváme na množinu M. Když množina M je prázdná, graf je souvislý. Protože algoritmem jsme prohledali všechny vrcholy, což znamená, že se z daného startovacího vrcholu umíme dostat do každého vrcholu, což je definice souvislosti. Když množina M není prázdná, graf není souvislý, protože do vrcholu, který zůstal v množině M se z daného startovacího vrcholu nedokážeme dostat a vrcholy spolu nesouvisí, teda nachází se v jiné komponentě souvislosti.
- Určení počtu komponent grafu:
- Princip:
- Nechť množina M = V(G). Spustíme prohledávání do hloubky nebo do šířky z prvního vrcholu množiny M a zvýšíme počet nalezených komponent na 1. APH (APŠ) postupně projde všechny vrcholy dosažitelné z daného vrcholu a po jejich zpracování je odstraní z množiny M. V množině M jsou v tento okamžik pouze ty vrcholy, které nepatřily do první komponenty. Algoritmus proto nalezne další vrchol v množině M, zvýší počet nalezených komponent a zpracuje daný vrchol pomocí APH (APŠ). Algoritmus končí v okamžiku, kdy už množina M neobsahuje žádný vrchol.
- Určení, zda vrcholy x,y spolu souvisí (tj. nachází se v jedné komponentě souvislosti):
- Princip:
- Spustíme prohledávání do hloubky nebo do šířky z vrcholu x (resp. y). APH (APŠ) postupně projde všechny vrcholy dosažitelné z daného vrcholu x (resp. y) a po jejich zpracování je vloží do množiny M. Po skončení algoritmu jsou v množině M ty vrcholy, které jsou dosažitelné z vrcholu x (resp. y). Když se v množině M nachází vrchol y (resp. x), vrcholy spolu souvisí, tj. nachází se v jedné komponentě souvislosti. Když se vrchol y (resp. x ) v množině M nenachází, vrcholy x a y se nachází v různých komponentách souvislosti a teda spolu nesouvisí.
- Určení, zda hrana e={x,y} je most:
- Princip:
- Nechť G´=G-e. V grafu G´ spustíme prohledávání do hloubky nebo do šířky z vrcholu x (resp. y). APH (APŠ) postupně projde všechny vrcholy dosažitelné z daného vrcholu x (resp. y) a po jejich zpracování je vloží do množiny M. Po skončení algoritmu jsou v množině M ty vrcholy, které jsou dosažitelné z vrcholu x (resp. y). Když se v množině M nachází vrchol y (resp. x), vrcholy spolu souvisí, tj. nachází se v jedné komponentě souvislosti v G´, což znamená, že existuje x,y cesta v G´. Cesta x,y spolu s hranou e={x,y} tvoří v G kružnici a teda hrana e={x,y} není most. Když se vrchol y (resp. x) v množině M nenachází, vrcholy x a y se nachází v různých komponentách souvislosti a hrana e={x,y} je most v G.
Doteď jsme mohli použít APŠ i APH. V následujících algoritmech si už nebudeme moc vybrat, který algoritmus použijeme.
- Určení vzdáleností a minimální cesty mezi danými vrcholy x,y:
- Princip:
- Spustíme prohledávání do šířky z vrcholu x (resp. y). APŠ postupně projde všechny vrcholy dosažitelné z daného vrcholu x (resp. y) a u každého vrcholu při jeho zpracování přiradí index, který informuje o tom, v jaké vzdáleností se nachází od prvního vrcholu. Když nás zajímá i cesta, můžeme vrcholu také přiradit informaci o předchozím vrcholu, čím zpětně nalezeme nejkratší cestu. Po skončení algoritmu se podíváme, jaký index je u vrcholu y (resp. x), ten udává vzdálenost mezi vrcholy x a y. Algoritmus můžeme ukončit v momentě, když zpracujeme vrchol y (resp. x).
- Určení, zda graf je bipartitní:
- Věta: Graf je bipartitní právě tehdy, když neobsahuje kružnici liché délky.
- Když najdeme v grafu lichou kružnici, graf není bipartitní. Spustíme prohledávání do šířky z libovolného vrcholu. APŠ postupně projde všechny vrcholy a u každého vrcholu při jeho zpracování přiradí index, který informuje o tom, v jaké vrstvě se vrchol nachází. U „červených hran“ kontroluje, zda spojuje vrcholy z jedné vrstvy nebo ze sousedních vrstev. Když všechny „červené hrany“ spojují vrcholy ze sousedních vrstev, graf neobsahuje lichou kružnici a graf je bipartitní. Když alespoň jedna „červená hrana“ spojuje vrcholy z jedné vrstvy, graf obsahuje lichou kružnici a není bipartitní. Algoritmus můžeme ukončit v momentě, když najdeme lichou kružnici.
- Určení, zda existuje kružnice obsahující daný vrchol x:
- Spustíme prohledávání do šířky z vrcholu x. APŠ postupně projde všechny vrcholy a u každého vrcholu při jeho zpracování přiradí index, který informuje o tom, v jakém podstromě se vrchol nachází. Každý soused vrcholu x dostane jiný index a ty označují podstromy. U „červených hran“ kontroluje, zda spojuje vrcholy z jednoho podstromu nebo z různých podstromů. Když alespoň jedna „červená hrana“ spojuje vrcholy z různých podstromů, graf obsahuje kružnici obsahující vrchol x. Když všechny „červené hrany“ spojují vrcholy v rámci jednoho podstromu, graf neobsahuje kružnici obsahující vrchol x. Algoritmus můžeme ukončit v momentě, když najdeme hranu, která spojuje vrcholy z různých podstromů.
- Určení, zda existuje kružnice obsahující danou hranu {x,y}:
- Spustíme prohledávání do šířky z vrcholu x. APŠ postupně projde všechny vrcholy a u každého vrcholu při jeho zpracování přiradí index, který informuje o tom, v jakém podstromě se vrchol nachází. Každý soused vrcholu x dostane jiný index a ty označují podstromy. U „červených hran“ kontroluje, zda spojuje vrchol z podstromu, který obsahuje vrchol y a nějaký vrchol z jiného podstromu . Když všechny „červené hrany“ spojují vrcholy v rámci jednoho podstromu nebo vrcholy z různých podstromů, ale ani jeden není podstrom obsahující vrchol y, graf neobsahuje kružnici obsahující hranu {x,y}. Když alespoň jedna „červená hrana“ spojuje vrchol z podstromu obsahující vrchol y a vrchol z jiného podstromu, graf obsahuje kružnici obsahující hranu {x,y}. Algoritmus můžeme ukončit v momentě, když najdeme hranu, která spojuje vrcholy z podstromu obsahujícího vrchol y a nějakého jiného podstromu.
Řešený příklad ⇫
1. Určete délku nejkratší cesty z vrcholu b do vrcholu j. Jednu cestu této délky vypište.
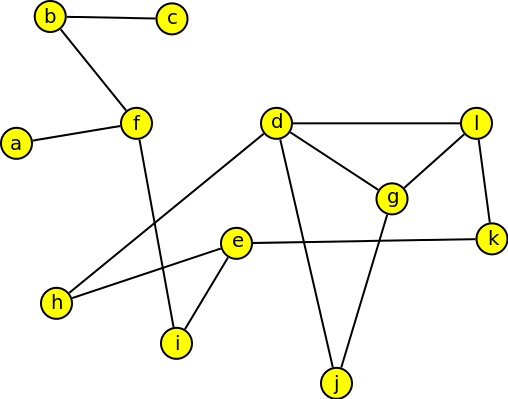
Krok 1
FIFO: b
Vrcholy: b(b0)
Krok 2
FIFO: b,c,f
Vrcholy: b(b0),c(b1),f(b1)
Krok 3
FIFO: b,c,f
Vrcholy: b(b0),c(b1),f(b1)
Krok 4
FIFO: b,c,f,a,i
Vrcholy: b(b0),c(b1),f(b1),a(f2),i(f2)
Krok 5
FIFO: b,c,f,a,i
Vrcholy: b(b0),c(b1),f(b1),a(f2),i(f2)
Krok 6
FIFO: b,c,f,a,i,e
Vrcholy: b(b0),c(b1),f(b1),a(f2),i(f2),e(i3)
Krok 7
FIFO: b,c,f,a,i,e,h,k
Vrcholy: b(b0),c(b1),f(b1),a(f2),i(f2),e(i3),h(e4),k(e4)
Krok 8
FIFO: b,c,f,a,i,e,h,k,d,l
Vrcholy: b(b0),c(b1),f(b1),a(f2),i(f2),e(i3),h(e4),k(e4),d(h5),l(k5)
Krok 9
FIFO: b,c,f,a,i,e,h,k,d,l,j
Vrcholy: b(b0),c(b1),f(b1),a(f2),i(f2),e(i3),h(e4),k(e4),d(h5),l(k5),j(d6)
Krok 10
Vrcholy: b(b0),c(b1),f(b1),a(f2),i(f2),e(i3),h(e4),k(e4),d(h5),l(k5),j(d6)
Nejkratší cesta z bodu b do bodu j má delku 6 a je to například cesta - b,f,i,e,h,d,j.
2. Určete z matice sousednosti, zda je graf souvislý. Graf nekreslete!
| A | B | C | D | E | F | |
| A | 1 | 1 | 1 | |||
| B | 1 | 1 | ||||
| C | 1 | 1 | ||||
| D | 1 | |||||
| E | 1 | |||||
| F | 1 |
Krok 1
Začneme v libovolném vrcholu prohledávání do hloubky (můžeme ale i do šířky). Začneme tedy například v A. Vložíme A do zásobníku. Vybereme nějakou hranu z vrcholu A, např. do B. B vložíme do Zásobníku a škrtneme hranu AB a BA.
| A | B | C | D | E | F | |
| A | 1 | 1 | 1 | |||
| B | 1 | 1 | ||||
| C | 1 | 1 | ||||
| D | 1 | |||||
| E | 1 | |||||
| F | 1 |
V = {A,B,C,D,E,F}
LIFO: A,B
Komponenta: 1
Vrcholy:
Hrany: AB
Krok 2
Pokračujeme z vrcholu B do vrcholu C. Vkládáme C a škrtáme BC a CB.
| A | B | C | D | E | F | |
| A | 1 | 1 | 1 | |||
| B | 1 | 1 | ||||
| C | 1 | 1 | ||||
| D | 1 | |||||
| E | 1 | |||||
| F | 1 |
V = {A,B,C,D,E,F}
LIFO: A,B,C
Komponenta: 1
Vrcholy:
Hrany: AB,BC
Krok 3
Pokračujeme z vrcholu C. Můžeme pokračovat ale pouze do vrcholu A, který už v Zásobníku máme. Škrtáme proto hranu CA a AC. V Zásobníku škrtáme vrchol C a přesunujeme ho do Vrcholů.
| A | B | C | D | E | F | |
| A | 1 | 1 | 1 | |||
| B | 1 | 1 | ||||
| C | 1 | 1 | ||||
| D | 1 | |||||
| E | 1 | |||||
| F | 1 |
V = {A,B,C,D,E,F}
LIFO: A,B,C
Komponenta: 1
Vrcholy: C
Hrany: AB,BC,CA
Krok 4
V Zásobníku vybereme poslední neškrtnutý vrchol, tj. B a pokračujeme z něho. Z B ovšem pokračovat nikam nemůžeme, škrtáme ho tedy v Zásobníku a přidáváme do Vrcholů.
| A | B | C | D | E | F | |
| A | 1 | 1 | 1 | |||
| B | 1 | 1 | ||||
| C | 1 | 1 | ||||
| D | 1 | |||||
| E | 1 | |||||
| F | 1 |
V = {A,B,C,D,E,F}
LIFO: A,B,C
Komponenta: 1
Vrcholy: C,B
Hrany: AB,BC,CA
Krok 5
V Zásobníku vybereme poslední neškrtnutý vrchol, tj. A a pokračujeme z něho. Z A jdeme do E, škrtáme tedy hranu AE a EA a zapisujeme E do Zásobníku.
| A | B | C | D | E | F | |
| A | 1 | 1 | 1 | |||
| B | 1 | 1 | ||||
| C | 1 | 1 | ||||
| D | 1 | |||||
| E | 1 | |||||
| F | 1 |
V = {A,B,C,D,E,F}
LIFO: A,B,C,E
Komponenta: 1
Vrcholy: C,B
Hrany: AB,BC,CA,AE
Krok 6
Z vrcholu E nemůžeme nikam pokračovat, škrtáme ho v Zásobníku, zapisujeme do Vrcholů. Pokračujeme posledním neškrtnutým vrcholem v Zásobníku, tj. A. Bohužel ani z A nemůžeme nikam pokračovat, proto ho v Zásobníku škrtáme a také zapisujeme do Vrcholů. Jelikož v Zásobníku již nemáme žádný neškrtnutý vrchol, s prohledáváním končíme a ve Vrcholech máme souvislou komponentu. Jak ale vidíme, máme zde zpracované pouze čtyři vrcholy, proto můžeme prohlásit, že tento graf není souvislý.
| A | B | C | D | E | F | |
| A | 1 | 1 | 1 | |||
| B | 1 | 1 | ||||
| C | 1 | 1 | ||||
| D | 1 | |||||
| E | 1 | |||||
| F | 1 |
V = {A,B,C,D,E,F}
LIFO: A,B,C,E
Komponenta: 1
Vrcholy: C,B,E,A
Hrany: AB,BC,CA,AE
3. Určete z matice sousednosti počet komponent grafu. Graf nekreslete!
| A | B | C | D | E | F | |
| A | 1 | 1 | 1 | |||
| B | 1 | 1 | ||||
| C | 1 | 1 | ||||
| D | 1 | |||||
| E | 1 | |||||
| F | 1 |
Krok 1
Postupujeme stejně, jako v příkladu 1. Ve Vrcholech máme jednu komponentu. Smažeme Zásobník a pokračujeme v prohledávání na zbylých vrcholech. Pokračujeme tedy ve vrcholu D. Zapíšeme ho do Zásobníku a vybereme nějakou hranu, v tomto případě do vrcholu F. Do Zásobníku zapisujeme F a škrtáme hrany DF a FD.
| A | B | C | D | E | F | |
| A | 1 | 1 | 1 | |||
| B | 1 | 1 | ||||
| C | 1 | 1 | ||||
| D | 1 | |||||
| E | 1 | |||||
| F | 1 |
V = {A,B,C,D,E,F}
LIFO: D,F
Komponenta: 1
Vrcholy: C,B,E,A
Hrany: AB,BC,CA,AE
Komponenta: 2
Vrcholy:
Hrany:DF
Krok 2
Stejně jako v předchozím příkladu, pokud již z vrcholu nemáme kam jít, vrchol v Zásobníku škrtáme a zapisujeme do Vrchulů. V tomto případě škrtáme F a zapisujeme do Vrcholů 2. Vracíme se do D, ale odtud také nemáme kam pokračovat. Škrtáme D a přesouváme také do Vrcholů 2. Tak nám vzniknou dvě skupiny Vrcholy, kdy v každé je jedna komponenta grafu. jelikož v matici již nemáme žádnou volnou hranu, můžeme prohlásit, že graf má dvě komponenty.
| A | B | C | D | E | F | |
| A | 1 | 1 | 1 | |||
| B | 1 | 1 | ||||
| C | 1 | 1 | ||||
| D | 1 | |||||
| E | 1 | |||||
| F | 1 |
V = {A,B,C,D,E,F}
LIFO:D,F
Komponenta: 1
Vrcholy: C,B,E,A
Hrany: AB,BC,CA,AE
Komponenta: 2
Vrcholy: F,D
Hrany:DF
4. Určete z matice sousednosti, zda vrcholy B a E spolu souvisejí. Graf nekreslete!
| A | B | C | D | E | F | |
| A | 1 | 1 | 1 | |||
| B | 1 | 1 | ||||
| C | 1 | 1 | ||||
| D | 1 | |||||
| E | 1 | |||||
| F | 1 |
Krok 1
Spustíme prohledávání z vrcholu B. Pokud se vrchol E objeví v prohledávání, souvisí s vrcholem B. Pokud se v prohledávání neobjeví, pak s vrcholem B nesouvisí. Zapíšeme tedy vrchol B do Zásobníku. Vybereme nějakou hranu z vrcholu B, například hranu BA. Škrtáme tedy hranu BA a AB a vrchol A zapisujeme do Zásobníku.
| A | B | C | D | E | F | |
| A | 1 | 1 | 1 | |||
| B | 1 | 1 | ||||
| C | 1 | 1 | ||||
| D | 1 | |||||
| E | 1 | |||||
| F | 1 |
V = {A,B,C,D,E,F}
LIFO: B,A
Komponenta: 1
Vrcholy:
Hrany: BA
Krok 2
Pokračujeme z vrcholu A do vrcholu C. Zapisujeme C do Zásobníku a škrtáme hranu AC a CA.
| A | B | C | D | E | F | |
| A | 1 | 1 | 1 | |||
| B | 1 | 1 | ||||
| C | 1 | 1 | ||||
| D | 1 | |||||
| E | 1 | |||||
| F | 1 |
V = {A,B,C,D,E,F}
LIFO: B,A,C
Komponenta: 1
Vrcholy:
Hrany: BA,AC
Krok 3
Z vrcholu C máme pouze hranu do vrcholu B. Ze Zásobníku ale vidíme, že vrchol B jsme již zpracovávali, proto pouze škrtáme hranu CB a BC. V Zásobníku škrtáme vrchol C a pokračujeme z vrcholu A po hraně AE. Zapisujeme vrchol E do zásobníku a škrtáme hranu AE a EA.
| A | B | C | D | E | F | |
| A | 1 | 1 | 1 | |||
| B | 1 | 1 | ||||
| C | 1 | 1 | ||||
| D | 1 | |||||
| E | 1 | |||||
| F | 1 |
V = {A,B,C,D,E,F}
LIFO: B,A,C,E
Komponenta: 1
Vrcholy: C
Hrany: BA,AC,CB,AE
Krok 4
Z obsahu Zásobníku vidíme, že jsme se z vrcholu B dostali do vrcholu E, a to přes vrchol A. Můžeme tedy prohlásit, že vrcholy B a E spolu souvisejí.
5. V následujícím grafu zadaném maticí sousedností určete, zda hrana {E,D} je most. Graf nekreslete! Zapište datovou strukturu, kterou používáte (LIFO či FIFO).
| A | B | C | D | E | F | G | H | I | J | |
| A | 1 | 1 | ||||||||
| B | 1 | 1 | 1 | 1 | 1 | |||||
| C | 1 | 1 | ||||||||
| D | 1 | 1 | 1 | |||||||
| E | 1 | 1 | 1 | |||||||
| F | 1 | 1 | ||||||||
| G | 1 | 1 | ||||||||
| H | 1 | 1 | ||||||||
| I | 1 | 1 | 1 | |||||||
| J | 1 | 1 |
Krok 1
Metodou prohledávání do hloubky se pokusíme najít jinou, než přímou cestu {E,D}. Začneme například ve vrcholu D a vybereme jinou hranu, než tu do vrcholu E - např. B. Škrtnu hrany DB a BD a D vložím do zásobníku.
| A | B | C | D | E | F | G | H | I | J | |
| A | 1 | 1 | ||||||||
| B | 1 | 1 | 1 | 1 | 1 | |||||
| C | 1 | 1 | ||||||||
| D | 1 | 1 | 1 | |||||||
| E | 1 | 1 | 1 | |||||||
| F | 1 | 1 | ||||||||
| G | 1 | 1 | ||||||||
| H | 1 | 1 | ||||||||
| I | 1 | 1 | 1 | |||||||
| J | 1 | 1 |
V = {A,B,C,D,E,F,G,H,I,J}
LIFO: D
Komponenta: 1
Vrcholy:
Hrany: DB
Krok 2
Pokračujeme z B. Vybereme vrchol A, škrtáme hranu BA a AB a do Zásobníku vkládáme B.
| A | B | C | D | E | F | G | H | I | J | |
| A | 1 | 1 | ||||||||
| B | 1 | 1 | 1 | 1 | 1 | |||||
| C | 1 | 1 | ||||||||
| D | 1 | 1 | 1 | |||||||
| E | 1 | 1 | 1 | |||||||
| F | 1 | 1 | ||||||||
| G | 1 | 1 | ||||||||
| H | 1 | 1 | ||||||||
| I | 1 | 1 | 1 | |||||||
| J | 1 | 1 |
V = {A,B,C,D,E,F,G,H,I,J}
LIFO: D,B
Komponenta: 1
Vrcholy:
Hrany: DB,BA
Krok 3
Pokračujeme z A. Vybereme vrchol C, škrtáme hrany AC a CA a do Zásobníku vkládáme A.
| A | B | C | D | E | F | G | H | I | J | |
| A | 1 | 1 | ||||||||
| B | 1 | 1 | 1 | 1 | 1 | |||||
| C | 1 | 1 | ||||||||
| D | 1 | 1 | 1 | |||||||
| E | 1 | 1 | 1 | |||||||
| F | 1 | 1 | ||||||||
| G | 1 | 1 | ||||||||
| H | 1 | 1 | ||||||||
| I | 1 | 1 | 1 | |||||||
| J | 1 | 1 |
V = {A,B,C,D,E,F,G,H,I,J}
LIFO: D,B,A
Komponenta: 1
Vrcholy:
Hrany: DB,BA,AC
Krok 4
Pokračujeme z C. Vložíme C do Zásobníku - D,B,A,C. Bohužel nemáme odtud kam pokračovat. Škrtáme v Zásobníku C a vracíme se tedy k A - D,B,A,C. Z A ale také nemáme kam jít. Škrtáme tedy i A.
| A | B | C | D | E | F | G | H | I | J | |
| A | 1 | 1 | ||||||||
| B | 1 | 1 | 1 | 1 | 1 | |||||
| C | 1 | 1 | ||||||||
| D | 1 | 1 | 1 | |||||||
| E | 1 | 1 | 1 | |||||||
| F | 1 | 1 | ||||||||
| G | 1 | 1 | ||||||||
| H | 1 | 1 | ||||||||
| I | 1 | 1 | 1 | |||||||
| J | 1 | 1 |
V = {A,B,C,D,E,F,G,H,I,J}
LIFO: D,B,A,C
Komponenta: 1
Vrcholy: C,A
Hrany: DB,BA,AC
Krok 5
Pokračujeme z B. Vybereme vrchol I, škrtáme hrany BI a IB a do Zásobníku vkládáme I.
| A | B | C | D | E | F | G | H | I | J | |
| A | 1 | 1 | ||||||||
| B | 1 | 1 | 1 | 1 | 1 | |||||
| C | 1 | 1 | ||||||||
| D | 1 | 1 | 1 | |||||||
| E | 1 | 1 | 1 | |||||||
| F | 1 | 1 | ||||||||
| G | 1 | 1 | ||||||||
| H | 1 | 1 | ||||||||
| I | 1 | 1 | 1 | |||||||
| J | 1 | 1 |
V = {A,B,C,D,E,F,G,H,I,J}
LIFO: D,B,A,C,I
Komponenta: 1
Vrcholy: C,A
Hrany: DB,BA,AC,BI
Krok 6
Pokračujeme z I. Vybereme vrchol E, škrtáme hrany IE a EI a do Zásobníku vkládáme E. V Zásobníku máme jinou cestu z vrcholu D do vrcholu E, tudíž hrana {D,E} nemůže být most.
| A | B | C | D | E | F | G | H | I | J | |
| A | 1 | 1 | ||||||||
| B | 1 | 1 | 1 | 1 | 1 | |||||
| C | 1 | 1 | ||||||||
| D | 1 | 1 | 1 | |||||||
| E | 1 | 1 | 1 | |||||||
| F | 1 | 1 | ||||||||
| G | 1 | 1 | ||||||||
| H | 1 | 1 | ||||||||
| I | 1 | 1 | 1 | |||||||
| J | 1 | 1 |
V = {A,B,C,D,E,F,G,H,I,J}
LIFO: D,B,A,C,I,E
Komponenta: 1
Vrcholy: C,A
Hrany: DB,BA,AC,BI,IE
6. Určete z matice sousednosti, zda je graf G bipartitní. Graf nekreslete!
| A | B | C | D | E | F | |
| A | 1 | 1 | 1 | |||
| B | 1 | 1 | 1 | |||
| C | 1 | 1 | ||||
| D | 1 | 1 | ||||
| E | 1 | |||||
| F | 1 |
Krok 1
Pro určení, zda daný graf je či není bipartitní potřebujeme zjistit, zda se v grafu nachází kružnice liché délky. To zjistíme pomocí prohledávání grafu do šířky. Začneme ve vrcholu A. Vložíme ho do Fronty a zároveň do Vrcholů.
V = {A,B,C,D,E,F}
FIFO: A
Vrcholy: A
Hrany:
Krok 2
Z vrcholu A můžeme pokračovat do B,C a E. Škrtáme vrchol ve Frontě a hrany v matici. Vrcholy B,C,E vložíme do Fronty a do Vrcholů. Tam si ještě poznamenáme k jednotlivým vrcholům číslo vrstvy a z jakého vrcholu jsme k nim došli.
| A | B | C | D | E | F | |
| A | 1 | 1 | 1 | |||
| B | 1 | 1 | 1 | |||
| C | 1 | 1 | ||||
| D | 1 | 1 | ||||
| E | 1 | |||||
| F | 1 |
V = {A,B,C,D,E,F}
FIFO: A,B,C,E
Vrcholy: A,B1A,C1A,E1A
Hrany:
Krok 3
Podle Fronty pokračujeme z vrcholu B. Škrtáme ho ve Frontě a v matici hrany BC,CB,BD,DB. Vrcholy C,D zapíšeme do Fronty. Při zápisu vrcholu C ale vidíme, že již ve frontě je. Zkontrolujeme tedy index vrcholu, z kterého jsme tentokrát do vrcholu C přišli. Jedná se o vrchol B1A. Oba koncové vrcholy hrany B1AC1A mají stejný index. Podle Tvrzení 5 graf nemůže být bipartitní.
| A | B | C | D | E | F | |
| A | 1 | 1 | 1 | |||
| B | 1 | 1 | 1 | |||
| C | 1 | 1 | ||||
| D | 1 | 1 | ||||
| E | 1 | |||||
| F | 1 |
V = {A,B,C,D,E,F}
FIFO: A,B,C,E
Vrcholy: A,B1A,C1A,E1A
Hrany:
7. Určete z matice sousednosti, zda vrchol C leží na kružnici. Graf nekreslete!
| A | B | C | D | E | F | |
| A | 1 | 1 | ||||
| B | 1 | 1 | ||||
| C | 1 | 1 | 1 | |||
| D | 1 | 1 | ||||
| E | 1 | 1 | ||||
| F | 1 |
Krok 1
Spustíme prohledávání do šířky z vrcholu C. Vložíme ho do Fronty.
V = {A,B,C,D,E,F}
FIFO: C
Vrcholy:
Hrany:
Krok 2
Z vrcholu C jdeme do vrcholů B,D,E. Zapíšeme je do Fronty a Vrcholů, kde si poznamenáme jejich podstromy jako indexy. Hrany CB,BC,CD,DC a CE,ED škrtneme v matici a vrchol C ve Frontě.
| A | B | C | D | E | F | |
| A | 1 | 1 | ||||
| B | 1 | 1 | ||||
| C | 1 | 1 | 1 | |||
| D | 1 | 1 | ||||
| E | 1 | 1 | ||||
| F | 1 |
V = {A,B,C,D,E,F}
FIFO: C,B,D,E
Vrcholy: B1,D2,E3
Hrany:
Krok 3
Pokračujeme z vrcholu B. Škrtneme ho ve Frontě. Do Fronty zapíšeme vrcholy A a v matici škrtneme hranu BA a AB. Do Vrcholů zapíšeme vrchol A s indexem podstromu 1.
| A | B | C | D | E | F | |
| A | 1 | 1 | ||||
| B | 1 | 1 | ||||
| C | 1 | 1 | 1 | |||
| D | 1 | 1 | ||||
| E | 1 | 1 | ||||
| F | 1 |
V = {A,B,C,D,E,F}
FIFO: C,B,D,E,A
Vrcholy: B1,D2,E3,A1
Hrany:
Krok 4
Pokračujeme ve vrcholu D. Škrtáme ve Frontě a jdeme do vrcholu F. Ten zíšeme do Fronty a s indexem 2 do Vrcholů. V matici škrtneme hrany DF a FD.
| A | B | C | D | E | F | |
| A | 1 | 1 | ||||
| B | 1 | 1 | ||||
| C | 1 | 1 | 1 | |||
| D | 1 | 1 | ||||
| E | 1 | 1 | ||||
| F | 1 |
V = {A,B,C,D,E,F}
FIFO: C,B,D,E,A,F
Vrcholy: B1,D2,E3,A1,F2
Hrany:
Krok 5
Pokračujeme z vrcholu E. Pokračovat můžeme pouze do A. Škrtáme hranu EA a AE. Vrchol E škrtáme ve Frontě a vrchol A bychom měli zapsat do Vrcholů. Ten tam ale již leží a to s indexem 1. Máme tedy hranu E3A1, což nám říká, že spojuje vrcholy z různých podstromů a tudíž vrchol C, z kterého jsme spustili vyhledávání leží na kružnici.
| A | B | C | D | E | F | |
| A | 1 | 1 | ||||
| B | 1 | 1 | ||||
| C | 1 | 1 | 1 | |||
| D | 1 | 1 | ||||
| E | 1 | 1 | ||||
| F | 1 |
V = {A,B,C,D,E,F}
FIFO: C,B,D,E,A,F
Vrcholy: B1,D2,E3,A1,F2
Hrany:
8. Určete z matice sousednosti, zda hrana {C,D} leží na kružnici. Graf nekreslete!
| A | B | C | D | E | F | |
| A | 1 | 1 | ||||
| B | 1 | 1 | ||||
| C | 1 | 1 | 1 | |||
| D | 1 | 1 | ||||
| E | 1 | 1 | ||||
| F | 1 |
Krok 1
Začneme prohledávat do šířky ve vrcholu C. Vložíme ho do Fronty.
V = {A,B,C,D,E,F}
FIFO: C
Vrcholy:
Hrany:
Krok 2
Podle lexikografického pravidla pokračujeme z vrcholu C do vrcholu B. Škrtneme hranu CB a BC a vrchol B zapíšeme do Fronty a do Vrcholů s indexem podstromu 1. Budeme si zapisovat i procházené hrany s indexem podstromů u vrcholů.
| A | B | C | D | E | F | |
| A | 1 | 1 | ||||
| B | 1 | 1 | ||||
| C | 1 | 1 | 1 | |||
| D | 1 | 1 | ||||
| E | 1 | 1 | ||||
| F | 1 |
V = {A,B,C,D,E,F}
FIFO: C,B
Vrcholy: B1
Hrany: C0B1
Krok 3
Dále prohledáme vrcholy D,E. Vložíme je do Fronty a škrtneme hrany CD, DC, CE a EC. Vrchol D zapíšeme do Vrcholů s indexem 2 a vrchol E s indexem 3.
| A | B | C | D | E | F | |
| A | 1 | 1 | ||||
| B | 1 | 1 | ||||
| C | 1 | 1 | 1 | |||
| D | 1 | 1 | ||||
| E | 1 | 1 | ||||
| F | 1 |
V = {A,B,C,D,E,F}
FIFO: C,B,D,E
Vrcholy: B1,D2,E3
Hrany: C0B1,C0D2,C0E3
Krok 4
Z vrcholu C již není kam jít. Škrtáme ho ve Frontě a pokračujeme z vrcholu B do vrcholu A. Ten zapíšeme do Fronty, škrtneme hrany a do Vrcholů ho zapíšeme s indexem 1.
| A | B | C | D | E | F | |
| A | 1 | 1 | ||||
| B | 1 | 1 | ||||
| C | 1 | 1 | 1 | |||
| D | 1 | 1 | ||||
| E | 1 | 1 | ||||
| F | 1 |
V = {A,B,C,D,E,F}
FIFO: C,B,D,E,A
Vrcholy: B1,D2,E3,A1
Hrany: C0B1,C0D2,C0E3,B1A1
Krok 5
Vrchol B škrtáme ve Frontě a pokračujeme z vrcholu D do vrcholu F. Zapíšeme ho do Fronty, škrtneme hrany DF a FD a vrchol F rovněž zapíšeme do Vrcholů s indexem 2.
| A | B | C | D | E | F | |
| A | 1 | 1 | ||||
| B | 1 | 1 | ||||
| C | 1 | 1 | 1 | |||
| D | 1 | 1 | ||||
| E | 1 | 1 | ||||
| F | 1 |
V = {A,B,C,D,E,F}
FIFO: C,B,D,E,A,F
Vrcholy: B1,D2,E3,A1,F2
Hrany: C0B1,C0D2,C0E3,B1A1,D2F2
Krok 6
Z vrcholu D není kam jít, škrtáme ho ve Frontě a pokračujeme z vrcholu E do vrcholu A. Tento vrchol jsme ale již procházeli. Škrtáme hranu EA a zapíšeme ji do Hran. Podíváme se do výpisu hran a vidíme, že jediná hrana z vrcholu D (nepočítáme sledovanou hranu) je hrana D2F2, kde mají oba vrcholy stejný index. Leží tudíž ve stejném podstromu. Z toho vyplývá, že hrana CD neleží na kružnici.
| A | B | C | D | E | F | |
| A | 1 | 1 | ||||
| B | 1 | 1 | ||||
| C | 1 | 1 | 1 | |||
| D | 1 | 1 | ||||
| E | 1 | 1 | ||||
| F | 1 |
V = {A,B,C,D,E,F}
FIFO: C,B,D,E,A,F
Vrcholy: B1,D2,E3,A1,F2
Hrany: C0B1,C0D2,C0E3,B1A1,D2F2,E3A1
Úlohy k řešení ⇫
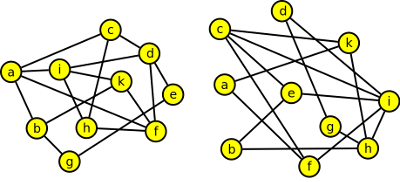
1. Prohledejte následující graf do šířky a do hloubky a výsledné grafy nakreslete.
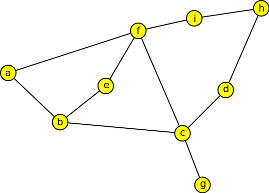
Výsledek


2. Algoritmem prohledávání
- do hloubky,
- do šířky
určete v grafech stromy prohledávání a vypište vrcholy v pořadí, v jakém budou zpracovány (navštíveny poprvé). Příslušné kořenové stromy prohledávání nakreslete.
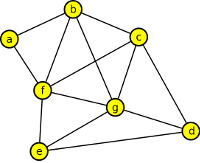
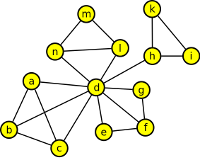
Výsledek
-
Vrcholy: a,b,c,d,e,f,g
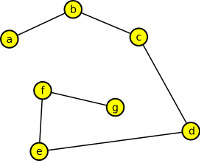
Vrcholy: a,b,f,c,g,e,d
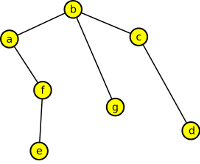
-
Vrcholy: a,b,c,d,e,f,g,h,i,k,l,m,n
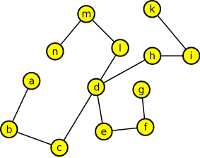
Vrcholy: a,b,c,d,e,f,g,h,l,n,i,k,m
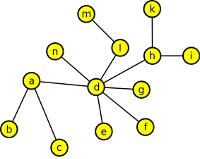
3. Pomocí vhodného algoritmu zjistěte, zda grafy jsou bipartitní:
Výsledek
1. graf:
| Vrcholy: | b1a | c1a | f1a | i1a | g2b | k2b | d2c | h2c | d2c | h2c | k2b | d2c | h2c | e3g | e3g |
| Hrany: | ab | ac | af | ai | bg | bk | cd | ch | fd | fh | fk | id | ih | ge | de |
Graf je bipartitní. Nejsou spojeny vrcholy ve stejné vrstvě kořenového stromu ⇒ není kružnice liché délky.
2. graf:
| Vrcholy: | f1a | k1a | c2f | i2f | c2f | h2k | e3c | i2f | |||||||
| Hrany: | af | ak | fc | fi | kc | kh | ce | ci |
Graf není bipartitní, protože v něm existuje hrana(ci), která spojuje dva vrcholy ze stejné vrstvy ⇒ existuje kružnice liché délky.
4. Vhodným algoritmem určete, zda vrcholy c,d leží v téže komponentě daného grafu či nikoli. Algoritmus stručně popište.
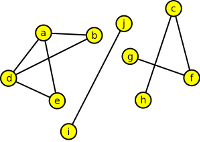
Výsledek
Za pomoci prohledávání do šířky nebo do hloubky z vrcholu c zjistíme, zda se v prohledávání objeví i vrchol d. Pokud ano, leží oba vrcholůy v téže komponentě.
| Zásobník: | c | f | g | h |
| Vrcholy: | c | f | g | h |
| Hrany: | cf | fg | ch |
Vrcholy c a d neleží v téže komponentě grafu.
Zdroje textů
- DIMA - diskrétní matematika, http://oliva.uhk.cz
- Hliněný, Petr. Diskrétní Matematika (456-533 DIM), 2006
- Kovář, Petr. DISKRÉTNÍ MATEMATIKA a ÚVOD DO TEORIE GRAFŮ ( příklady k procvičení ), 2012