Eulerovské grafy
Teorie ⇫
Ve městě Kőnigsbergu (česky nazývaném Královec, dnešním Kaliningradu) jsou v centru města na řece Pregel (dnes Pregolya) dva ostrovy, které v 18. století spojovalo s oběma břehy sedm mostů (viz obrázek níže). Obyvatelé města při nedělní procházce často přemýšleli, zda by bylo možné projít se městem tak, že by procházku začali v jednom místě, přešli všechny mosty, přes každý právě jednou a skončili by tam, kde začali. Protože se jim však stále nedařilo najít způsob, jakým by to provedli, začali se mnozí z nich domnívat, že takovou procházku ani uskutečnit nejde. Tento názor byl matematicky potvrzen roku 1736, kdy byl uvedený problém předložen k vyřešení vynikajícímu švýcarskému matematikovi, Leonhardu Eulerovi. Leonhard Euler nejen tento konkrétní problém vyřešil, ale podal obecnou charakteristiku úloh daného typu.
Sedm mostů v Kőnigsbergu
Pozn.: Uvedený problém je považován za první příspěvek k teorii grafů a rok 1736 je pokládán za počátek teorie grafů.
Definice eulerovského tahu:
Eulerovským tahem v grafu G nazveme každý tah, který obsahuje všechny hrany grafu G.
Pozn.: Eulerovský tah nám umožňuje projít celým grafem, každou hranou právě jednou.
Definice eulerovského grafu:
Eulerovským grafem nazýváme každý souvislý graf, ve kterém existuje eulerovský tah.
Pozn.: Eulerovský graf lze nakreslit jedním tahem.
Eulerovský graf je charakterizován následující větou:
- Věta:
Graf je eulerovský, právě když je souvislý a má buď všechny vrcholy sudého stupně nebo právě dva vrcholy stupně lichého.
- Důkaz:
Nechť G je eulerovský graf. Pak dle definice o eulerovskem tahu v něm existuje tah T obsahující všechny hrany grafu G. Odtud je zřejmé, že graf G je souvislý. Je-li tah T uzavřený, znamená to, že všechny vrcholy jsou sudého stupně, neboť pro každý vrchol v grafu platí degG(v)=2∙p, kde p je počet výskytů vrcholu v v tahu T. Není-li tah T uzavřený, pak právě dva vrcholy grafu mají lichý stupeň (koncové vrcholy tahu T).∎
Pro důkaz druhé implikace dokažme nejprve několik následujících tvrzení, přičemž pro jednoduchost vyjadřování nazýváme graf, jehož všechny vrcholy mají sudý stupeň, sudý graf.
- Důkaz provedeme sporem:
-
⇒ Nechť G=(V,E) je sudý graf. Předpokládejme pro spor, že hrana e={v,w} je most komponenty Q grafu G (je-li graf G souvislý, je Q=G).
Odebráním hrany e z komponenty Q dostaneme dvě nové komponenty grafu G. Označme Q1 tu, která obsahuje vrchol v (pro druhou komponentu, která obsahuje vrchol w, bychom postupovali analogicky) a podívejme se na skóre této komponenty. Všechny vrcholy komponenty Q1, s výjimkou vrcholu v, mají původní sudý stupeň. Vrchol v (po odebrání hrany e) je zřejmě jediný vrchol lichého stupně. Odtud dostáváme ihned spor, protože, jak víme z důsledku vety o sudosti (Počet vrcholů lichého stupně v grafu je sudý.), v každém grafu musí být počet vrcholů lichého stupně sudý.∎
- Důkaz:
⇒ Důkaz plyne ihned z předchozího Tvrzení 1 a ze zřejmé skutečnosti, že když hrana není most, pak leží na nějaké kružnici (důkaz věty o ekvivalentních podmínkách ve stromech).∎
- Tvrzení 3:
Každý sudý graf lze zapsat jako sjednocení kružnic, které jsou navzájem po dvou hranově disjunktní.
- Důkaz:
⇒ Nechť G=(V,E) je sudý graf a e jeho libovolná hrana. Z předchozího Tvrzení 2 víme, že každá hrana leží na nějaké kružnici. Uvažujme kružnici C obsahující hranu e. Vyjmeme-li všechny hrany kružnice C z grafu G, dostaneme graf G', který je opět sudý, neboť stupeň každého vrcholu ležícího na kružnici C se vyjmutím hran kružnice C sníží o dvě. Postup opakujeme tak dlouho, až dostaneme diskrétní graf G*=(V,∅). Sjednocením postupně odebíraných kružnic dostaneme původní graf G.
Důkaz věty (druhé implikace) dokážeme indukcí podle počtu hran grafu.
Nejprve uvažujme souvislý sudý graf, tj. dokazujeme větu:
- G je souvislý a sudý G ⇒ je eulerovský
- Souvislý sudý graf obsahující tři hrany je zřejmě kružnice délky tři, tedy tento graf eulerovský je.
- Nechť věta platí pro souvislý sudý graf s m hranami, m≥3 . Dokážeme ji i pro souvislý sudý graf G s (m+1) hranami.
Podle Tvrzení 3 lze graf G chápat jako sjednocení kružnic navzájem po dvou hranově disjunktních. Nechť C je libovolná z těchto kružnic. Vynecháme-li z grafu G hrany kružnice C, pak vzniklý graf nemusí být souvislý, ale v každé jeho komponentě existuje dle indukčního předpokladu uzavřený eulerovský tah. Tyto tahy můžeme pospojovat spolu s kružnicí C do uzavřeného tahu obsahujícího všechny hrany grafu G, tj. G je eulerovský.
Nyní dokážeme větu ještě i pro souvislý graf G=(V,E) s právě dvěma vrcholy lichého stupně, a to tak, že daný graf převedeme na sudý graf.
Nechť vrcholy x, y jsou lichého stupně. Pro vrcholy x,y platí právě jedna ze dvou možností:
- buď vrcholy x,y netvoří hranu grafu G, tj. {x,y}∉E
- nebo hrana mezi nimi existuje, tj. {x,y}∈E
V prvním případě spojíme „pomocnou“ hranou e vrcholy x a y, čímž dostaneme souvislý sudý graf, ve kterém podle již dokázaného existuje uzavřený eulerovský tah T=(x,y,v,...,x). Odtud je zřejmé, že tah T–e=(y,...,x) je otevřeným eulerovským tahem v grafu G a tudíž graf G je eulerovský graf.
V druhém případě spojíme vrcholy x,y s novým vrcholem v*, čímž dostaneme souvislý sudý graf G´=(V∪v*, E∪{x,v*}∪{y,v*}). Obdobně jako v předchozím případě v grafu G´ existuje uzavřený eulerovský tah T=(v*,x,...,y,v*), a pak tah T–({y,v*}, v*, {v*,x}) je otevřeným eulerovským tahem (x,...,y) v grafu G a tudíž graf G je eulerovský graf.∎
Jak nalézt eulerovský tah
Zamysleme se, co můžeme tvrdit o eulerovském grafu, tj. souvislém grafu, jehož všechny vrcholy jsou stupně sudého nebo právě dva vrcholy stupně lichého:
- V případě všech vrcholů stupně sudého najdeme v grafu nějaký uzavřený tah, obsahuje-li graf právě dva vrcholy stupně lichého, tak v něm najdeme nějaký otevřený tah začínající v jednom z lichých vrcholů a končící v druhém z nich.
- Jestliže nalezený tah obarvíme, tak ve zbylé neobarvené části grafu (ta již nemusí být souvislá) jsou všechny vrcholy stupně sudého (zamyslete se proč!), tudíž v této části můžeme nalézt nějaký další uzavřený tah. Obarvíme ho jinou barvou. Takto můžeme analogicky postupovat tak dlouho, dokud neobarvíme všechny hrany grafu. Na eulerovský graf lze tudíž pohlížet jako na sjednocení tahů, a to buď všech uzavřených tahů nebo všech uzavřených s výjimkou jediného prvního otevřeného tahu.
- Vzhledem k souvislosti eulerovského grafu musí mít každý tah alespoň jeden vrchol společný s alespoň jedním jiným tahem.
Pro počítačové zpracování je zásadní otázka, jak efektivně napojit jednotlivé tahy na sebe. Odpověď nalezneme v Edmonds-Johnsonovu algoritmu procházení labyrintem. Aplikujeme-li tento přístup na eulerovské grafy, je zřejmé, že „zpětný průchod“ hranami (pořadí hran při „zpětném průchodu“) určuje tah, který prochází všemi hranami daného grafu, tj. eulerovský tah.
Na základě výše napsaného můžeme celý proces (algoritmus) hledání jednotlivých tahů a jejich napojování do výsledného eulerovského tahu popsat následovně:
- Uvažujme eulerovský graf.
- Představme si, že modrou pastelkou začneme ve vrcholu x kreslit nějaký tah, dokud to jde. Je zřejmé, že vytvoříme buď uzavřený tah končící ve vrcholu x nebo otevřený tah končící ve vrcholu y, přičemž neobarvené hrany tvoří sudý graf.
- Nyní se po vytvořeném tahu vracejme zpět do prvního vrcholu x1, který je incidentní s nějakou ještě neobarvenou hranou, a tuto zpáteční cestu zaznamenávejme červenou pastelkou. Pak pokračujme v neobarvené části v kreslení dalšího modrého tahu z x1 tak dlouho, dokud je to možné. Je zřejmé, že skončíme ve vrcholu x1 (tvoříme uzavřený tah). A opět se vracejme zpět do prvního vrcholu, který je incidentní s nějakou ještě neobarvenou hranou, a tuto zpáteční cestu zaznamenávejme červenou pastelkou.
- Opakujme popsaný proces tak dlouho, dokud v grafu existují neobarvené hrany.
- Zpáteční cesta zaznamenávaná červenou pastelkou tvoří výsledný eulerovský tah, neboť jednotlivé úseky kreslené červenou pastelkou (zpětný průchod po modře vytvořených tazích) na sebe vždy navazují.
Příklad
V následujícím grafu najděte Eulerovský tah.
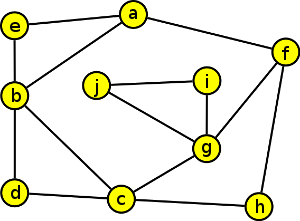
Tento problém řešíme pomocí postupu, který jsme právě popsali:
- V grafu začneme modře obarvovat tah začínající v některém vrcholu lichého stupně. V našem případě vrchol a.
- Pokračujeme v modrém obarvování, dokud je to možné.
- Pokud již nemůžeme pokračovat, vracíme se do vrcholu, který je incidentní s nějakou neobarvenou hranou a tuto zpáteční cestu obarvujeme červeně.
- V neobarveném podgrafu pokračujeme v hledání Eulerova tahu a obarvujeme modře.
- Pokud již nemáme v grafu žádnou neobarvenou hranu, máme nalezen Eulerovský tah. Ten je tvořen střídáním modrého a červeného podgrafu.
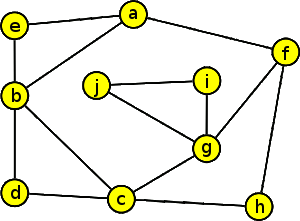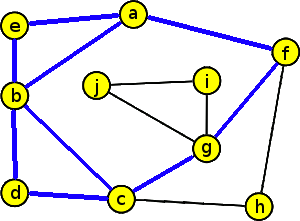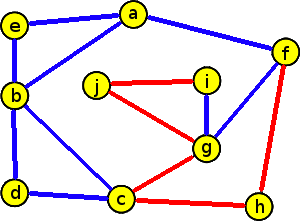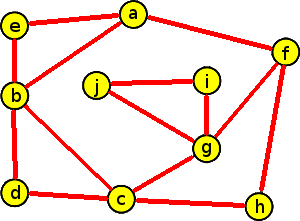
Z hlediska počítačového zpracování je výhodné použít pro zaznamenávání popsaného procesu datovou struktura zásobník. Postupně vkládané vrcholy do zásobníku Z určují jednotlivé tahy (kreslení modrou pastelkou) a postupně ze zásobníku Z odebírané vrcholy ukládané do dalšího zásobníku TAH určují výsledný eulerovský tah („zpětný průchod“ hranami kreslený červenou pastelkou).
Algoritmus nalezení eulerovského tahu
Nechť je dán eulerovský graf G=(V,E) s n vrcholy a m hranami. Nechť vrchol v je vrchol množiny V, přičemž jsou-li všechny vrcholy grafu G sudého stupně, pak v je libovolný vrchol, má-li graf G právě dva vrcholy stupně lichého, je v jeden z nich. Úkolem je nalézt a vypsat eulerovský tah grafu G.
začátek
na počátku nechť je každá hrana grafu G neobarvená. Nechť zásobník Z a zásobník TAH je prázdný. Vlož vrchol v do zásobníku Z;
dokud zásobník Z je neprázdný opakuj
začátek
x : = vrchol ležící na posledním místě v zásobníku;
jestliže x je koncový vrchol neobarvené hrany {x,y} pak
začátek
zpracuj hranu {x,y} a obarvi ji modře;
vlož vrchol y do zásobníku;
konec
jinak (tj. v případě, že x není koncovým vrcholem žádné neobarvené hrany)
začátek
odeber vrchol x ze zásobníku Z;
vlož vrchol x do zásobníku TAH;
konec;
konec;
V zásobníku TAH je uložen eulerovský tah.
konec.
Pozn.: Výsledný eulerovský tah uložený v zásobníku TAH můžeme číst jak od začátku, tak od konce.
Příklad
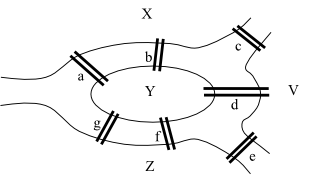
Nalezněte Eulerovský tah pro následující graf.
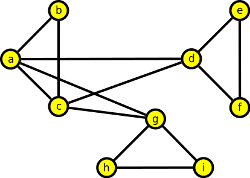
- nalezení tahu T1=(a,b,c,a,d,c,g,a) ━━━━
- návrat z vrcholu a do vrcholu g, uložení vrcholu a do zásobníku TAH, konstrukce tahu T2=(g,h,i,g) ━━━━
- návrat po celém tahu T2 a po tahu T1 do vrcholu d, uložení vrcholů g,i,h,g,c do zásobníku TAH, konstrukce tahu T3=(d,e,f,d) ━━━━
- návrat po celém tahu T3 a po tahu T1 až do počátečního vrcholu a, uložení vrcholů d,f,e,d,a,c,b,a do zásobníku TAH
-
TAH=(a,g,i,h,g,c,d,f,e,d,a,c,b,a)
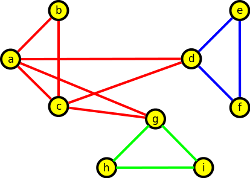
Ilustrace činnosti algoritmu pro předchozí graf zadaném maticí sousedností:
| a | b | c | d | e | f | g | h | i | |
| a | 1 | 1 | 1 | 1 | |||||
| b | 1 | 1 | |||||||
| c | 1 | 1 | 1 | 1 | |||||
| d | 1 | 1 | 1 | 1 | |||||
| e | 1 | 1 | |||||||
| f | 1 | 1 | |||||||
| g | 1 | 1 | 1 | 1 | |||||
| h | 1 | 1 | |||||||
| i | 1 | 1 |
Vrchol a vložíme do zásobníku, podíváme se v matici, do kterého vrcholu jde z a hrana, jde do vrcholu b, vrchol b vložíme do zásobníku a v matici škrtnu hranu ab a ba, přejdu na řádek s vrcholem b a podívám se kam jde hrana, do vrcholu c, c vložím do zásobníku a tak pokračujeme… ,až dostaneme:
| a | b | c | d | e | f | g | h | i | |
| a | 1 | 1 | 1 | 1 | |||||
| b | 1 | 1 | |||||||
| c | 1 | 1 | 1 | 1 | |||||
| d | 1 | 1 | 1 | 1 | |||||
| e | 1 | 1 | |||||||
| f | 1 | 1 | |||||||
| g | 1 | 1 | 1 | 1 | |||||
| h | 1 | 1 | |||||||
| i | 1 | 1 |
LIFO: a,b,c,a,d,c,g,a
ET:
Teď už nemáme kam z vrcholu a jít, vrchol a vyjmeme ze zásobníku a vložíme do ET (eulerovský tah), pak pokračujeme vrcholem g, z g do h, h dáme do zásobníku a smažeme hrany gh, hg v matici a pokračujeme vrcholem h….
Takto pokračujeme dokud nenarazíme opět na vrchol, z kterého už nemůžeme pokračovat. Daný vrchol vyndáme ze zásobníku a dáme do ET. Stejným způsobem pokračujeme, dokud není zásobník prázdny. V ET je eulerovský tah, který můžeme číst jak zepředu, tak zezadu.
Lifo: a,b,c,a,d,c,g,a,h,i,g,e,f,d ET: a,g,i,h,g,c,d,f,e,d,a,c,b,a
Řešený příklad ⇫
1. Je možné nakreslit graf K3,3, kterému chybí jedna hrana, jedním tahem?
Krok 1
chybí-li grafu jedna hrana, je jeho skóre (2,2,3,3,3,3)
Krok 2
ze skóre vidíme, že takovýto graf neobsahuje pouze dva vrcholy lichého stupně
Krok 3
můžeme prohlásit, že bipartitní graf K3,3, kterému chybí jedna hrana nejde nakreslit jedním tahem.
2. Najděte Eulerovský tah pro graf zadaný maticí sousedností:
| a | b | c | d | e | f | g | h | |
| a | 1 | 1 | ||||||
| b | 1 | 1 | ||||||
| c | 1 | 1 | 1 | 1 | ||||
| d | 1 | 1 | ||||||
| e | 1 | 1 | ||||||
| f | 1 | 1 | ||||||
| g | 1 | 1 | ||||||
| h | 1 | 1 |
Krok 1
Vrchol a vložím do zásobníku. LIFO: a.
Krok 2
podívám se v matici, do kterého vrcholu jde z a hrana. Jde do vrcholu b, vrchol b vložím do zásobníku a v matici škrtnu nebo smažu hranu ab a ba.
| a | b | c | d | e | f | g | h | |
| a | 1 | |||||||
| b | 1 | |||||||
| c | 1 | 1 | 1 | 1 | ||||
| d | 1 | 1 | ||||||
| e | 1 | 1 | ||||||
| f | 1 | 1 | ||||||
| g | 1 | 1 | ||||||
| h | 1 | 1 |
LIFO: a,b
ET:
Krok 3
Přejdu na řádek s vrcholem b a pokračuji do vrcholu h. Vložím do zásobníku a smažu hranu bh a hb.
| a | b | c | d | e | f | g | h | |
| a | 1 | |||||||
| b | ||||||||
| c | 1 | 1 | 1 | 1 | ||||
| d | 1 | 1 | ||||||
| e | 1 | 1 | ||||||
| f | 1 | 1 | ||||||
| g | 1 | 1 | ||||||
| h | 1 |
LIFO: a,b,h
ET:
Krok 4
...a tak pokračujeme, až dostaneme:
| a | b | c | d | e | f | g | h | |
| a | ||||||||
| b | ||||||||
| c | 1 | 1 | ||||||
| d | ||||||||
| e | 1 | 1 | ||||||
| f | 1 | 1 | ||||||
| g | 1 | 1 | ||||||
| h |
LIFO: a,b,h,d,c,a
ET:
Krok 5
Teď už nemáme kam z vrcholu a jít, vrchol vyjmeme ze Zásobníku a vložíme do ET (eulerovský tah). LIFO: a,b,h,d,c. ET: a.
Krok 6
Pak pokračujeme vrcholem c. Z c jdeme do e, e dáme do Zásobníku a smažeme hrany ce, ec v matici.
| a | b | c | d | e | f | g | h | |
| a | ||||||||
| b | ||||||||
| c | 1 | |||||||
| d | ||||||||
| e | 1 | |||||||
| f | 1 | 1 | ||||||
| g | 1 | 1 | ||||||
| h |
LIFO: a,b,h,d,c,e
ET: a
Krok 7
Pokračujeme vrcholem e. Jdeme do g. Mažeme hranu eg a ge a g dáme do Zásobníku.
| a | b | c | d | e | f | g | h | |
| a | ||||||||
| b | ||||||||
| c | 1 | |||||||
| d | ||||||||
| e | ||||||||
| f | 1 | 1 | ||||||
| g | 1 | |||||||
| h |
LIFO: a,b,h,d,c,e,g
ET: a
Krok 8
Z vrcholu g pokračujeme do f. Mažeme hrany a vrchol f zapisujeme do Zásobníku.
| a | b | c | d | e | f | g | h | |
| a | ||||||||
| b | ||||||||
| c | 1 | |||||||
| d | ||||||||
| e | ||||||||
| f | 1 | |||||||
| g | ||||||||
| h |
LIFO: a,b,h,d,c,e,g,f
ET: a
Krok 9
Z vrcholu f můžeme pokračovat do vrcholu c. Zapíšeme tedy c do Zásobníku a mažeme hrany fc a cf.
| a | b | c | d | e | f | g | h | |
| a | ||||||||
| b | ||||||||
| c | ||||||||
| d | ||||||||
| e | ||||||||
| f | ||||||||
| g | ||||||||
| h |
LIFO: a,b,h,d,c,e,g,f,c
ET: a
Krok 10
Z c ale již nikam pokračovat nemůžeme. Přesuneme tedy c ze Zásobníku do ET. Pokračujeme vrcholem f. Z něho také nemůžeme pokračovat a tak ho přesuneme do ET. Tak nakonec převedeme všechny vrcholy ze Zásobníku do ET. Nakonec je tedy Zásobník prázdny a v ET je eulerovský tah. Ten můžeme číst jak zepředu, tak zezadu. LIFO: . ET: a,c,f,g,e,c,d,h,b,a
Úlohy k řešení ⇫
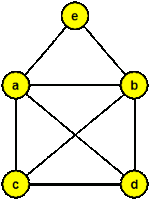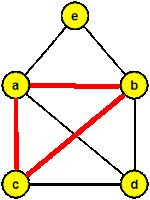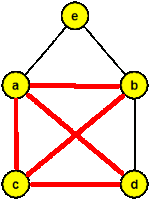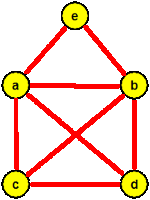
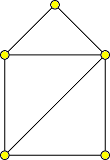
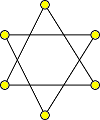
1. Rozhodněte, který z těchto grafů je eulerovský, který není a proč.
 |
 |
 |
| a | b | c |
Výsledek
a - ano, b - ano, c - ne, protože není souvislý.
2. Kolik nejméně hran je třeba přidat do grafu K3,3 − e, aby jej bylo možno nakreslit jedním otevřeným tahem?
Výsledek
Jednu a to mezi vrcholy stupně 3.
3. Rozhodněte, zda posloupnost (1,1,2,2,2,3,3,4) může být skóre eulerovského grafu. Své rozhodnutí zdůvodněte.
Výsledek
Ne, protože skóre obsahuje více než dva vrcholy lichého stupně.
4. Ve městě, které se rozkládá na třech ostrovech A,B,C a dvou březích D,E jedné řeky, bylo vybudováno osm mostů následovně: A je spojené s B dvěma mosty, C je spojené s D dvěma mosty, A je spojené s E jedním mostem, A je spojené s C jedním mostem, B je spojené s C jedním mostem a jeden most spojuje břehy E a D. Každý z pěti spolužáků bydlících v právě jedné části města (A,B,C,D,E) mělo na návštěvě hosty. Spolužáci se rozhodli, že hosty provedou městem a přitom projdou každým mostem a svoji vycházku ukončí v cukrárně na ostrově B. Zjistěte, zda se některému ze spolužáků podařilo projít se svými hosty město tak, že prošli každým mostem právě jednou a vycházku ukončí na ostrově B.
Výsledek
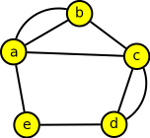
Podaří se to pouze spolužákovi z části D, protože do jeho části vedou tři mosty stejně jako do části B, kde mají vycházku ukončit. Jak víme, eulerovský tah začíná a končí ve vrcholech lichého stupně, vyskytují-li se v grafu.
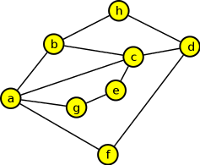
5. V následujících grafech najděte eulerovské tahy, použijte algoritmus:
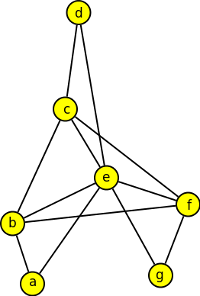
Výsledek
ET: d,f,a,g,e,c,d,h,b,c,a,b; ET: a,b,c,d,e,b,f,c,e,f,g,e,a
6. V následujícím grafu zadaném maticí najděte eulerovský tah, použijte algoritmus:
| a | b | c | d | e | f | g | h | |
| a | 1 | 1 | 1 | |||||
| b | 1 | 1 | 1 | 1 | ||||
| c | 1 | 1 | 1 | |||||
| d | 1 | 1 | 1 | 1 | ||||
| e | 1 | 1 | ||||||
| f | 1 | 1 | ||||||
| g | 1 | 1 | ||||||
| h | 1 | 1 |
Výsledek
ET: c,e,g,a,f,d,h,b,d,c,b,a
Zdroje textů
- DIMA - diskrétní matematika, http://oliva.uhk.cz
- Hliněný, Petr. Diskrétní Matematika (456-533 DIM), 2006
- Kovář, Petr. DISKRÉTNÍ MATEMATIKA a ÚVOD DO TEORIE GRAFŮ ( příklady k procvičení ), 2012