Rovinné grafy
Teorie ⇫
Definice rovinného grafu:
Graf je rovinný graf, jestliže k němu existuje tzv. rovinná reprezentace (rovinné nakreslení) - tj. můžeme jej nakreslit do roviny tak, aby se žádné dvě hrany neprotínaly ve vnitřním bodě (hrany se mohou protínat jen ve vrcholech).
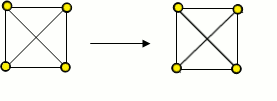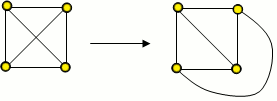
Graf G je rovinný, protože existuje jeho rovinné nakreslení.
Příklady Rovinných grafů:
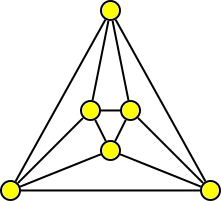
Také platónská tělesa lze nakreslit jako rovinný graf.
Platónské těleso
V geometrii je Platónské těleso pravidelný konvexní mnohostěn (polyedr) v prostoru, tj. z každého vrcholu vychází stejný počet hran a všechny stěny tvoří shodné pravidelné mnohoúhelníky.
Zde je ukázka všech pěti Platónských těles:
| Čtyřstěn | Šestistěn | Osmistěn | Dvanáctistěn | Dvacetistěn |
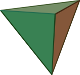 | 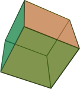 |  | 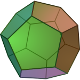 | 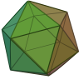 |
Definice stěny:
Nechť G je rovinný graf. V rovinném nakreslení grafu G uvažme množinu všech bodů roviny, které neleží v žádné hraně ani vrcholu. Tato množina se rozpadne na konečný počet souvislých oblastí, které nazýváme stěny rovinného grafu.

Graf má 4 stěny: F1,F2,F3,F4.
Pro rovinné grafy platí následovní věta:
- Věta (Eulerova):
Nechť G=(V,E) je souvislý rovinný graf, nechť F je množina stěn jeho rovinného nakreslení. Pak platí:
|F| = |E| - |V| + 2
Příklad
Graf pravidelného osmistěnu má 6 vrcholů a 8 stěn. Kolik má hran?
K vyřešení úlohy použijeme Eulerovu větu: |F| = |E| - |V| + 2
8 = |E| - 6 + 2 ⇒ |E| = 8 + 6 - 2 = 12
Graf pravidelného osmistěnu má 12 hran.

Důsledkem Eulerové věty jsou následující tvrzení, jejichž ekvivalentní tvrzení se využívají při dokazování, že graf není rovinný:
- Tvrzení 1
- Pro každý graf G = (V, E) s alespoň třemi vrcholy platí:
- Jestliže G je rovinný graf, pak |E|≤ 3|V|- 6.
- Ekvivalentní tvrzení:
- Pro každý graf G = (V, E) s alespoň třemi vrcholy platí:
- Jestliže |E| > 3|V|- 6, pak graf G není rovinný.
- Tvrzení 2
- Pro každý graf G = (V, E), který má alespoň tři vrcholy, a který neobsahuje K3 jako podgraf, platí:
- Jestliže G je rovinný graf, pak |E| ≤ 2|V| - 4.
- Ekvivalentní tvrzení:
- Pro každý graf G = (V, E), který má alespoň tři vrcholy, a který neobsahuje K3 jako podgraf, platí:
- Jestliže |E| > 2|V| - 4, pak graf G není rovinný.
Nejmenšími (na počet vrcholů) nerovinnými grafy jsou K5 a K3,3.
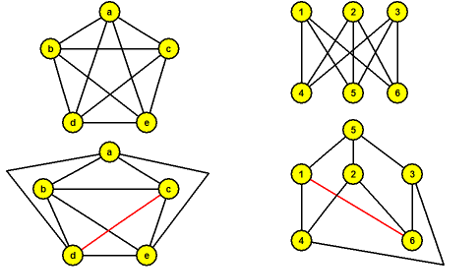
Pomocí předchozích tvrzení dokážeme, že nejsou rovinné:
- K5 je graf s min 3 vrcholy (obsahuje K3 jako podgraf), má 5 vrcholů a 10 hran, platí: 10 > 3.5 – 6, podle Tvrzení 1 graf K5 není rovinný
- K3,3 je graf s min 3 vrcholy a neobsahuje K3 jako podgraf, má 6 vrcholů a 9 hran, platí 9 > 2.6 - 4, podle Tvrzení 2 graf K3,3 není rovinný
Definice dělení hrany:
Nechť G=(V,E) je graf a e={x,y} jeho libovolná hrana. Řekneme, že graf G%e=(V∪{z},(E-e)∪{{x,z},{z,y}}, kde z∉V je graf vzniklý z grafu G dělením (nebo podrozdělením nebo půlením) hrany e.
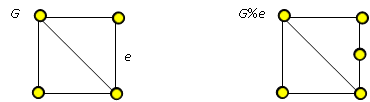
Definice dělení:
Nechť G=(V,E) je obyčejný graf. Dělením (podrozdělením) grafu G nazýváme každý graf, který vznikl z grafu G postupným dělením (podrozdělením) hran.
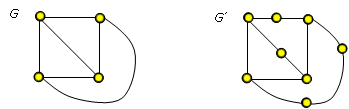
- Věta (Kuratowského):
Graf je rovinný právě tehdy, když žádný jeho podgraf není ani graf K3,3, ani graf K5, ani libovolné dělení (podrozdělením) těchto grafů.
Příklad
Kolik nejméně hran je třeba vypustit z následujícího 8-vrcholového grafu, aby vznikl rovinný graf?
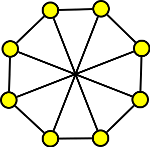
Zjistíme, zda graf náhodou není rovinný. Z následujícího obrázku vidíme, že obsahuje podgraf K3,3.
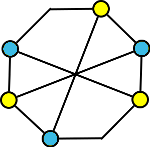
Z uvedeného obrázku ještě vidíme, že vypuštění vnitřní hrany z původního grafu rovinný graf nevznikne. Vypustíme-li ale hranu vnější, rovinný graf vznikne.
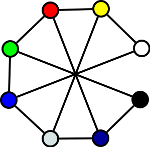
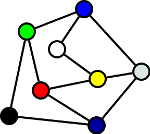
Praktické využití rovinných grafů je rozsáhlé (např. návrh elektrických obvodů). Existuje i rychlý algoritmus na zjištění, zda daný graf je rovinný.
Řešený příklad ⇫
1. Proč není graf G rovinný?
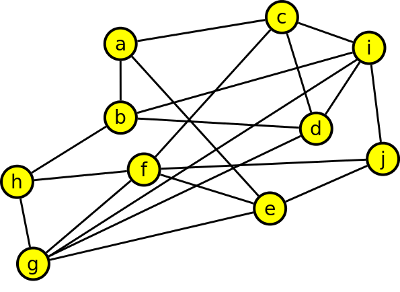
Krok 1
Protože obsahuje podgraf dělení grafu K5
Krok 2
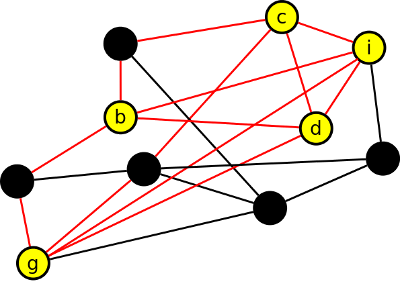
Krok 3
Nemůže být podle Kuratowského věty rovinný!
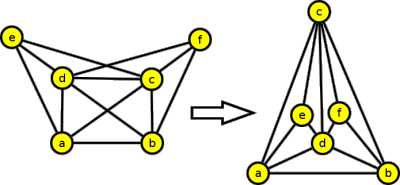
2. Rozhodněte, zda doplněk podgrafu indukovaného vrcholy {c,d,e,f,g} grafu G je nebo není rovinný graf. Své rozhodnutí zdůvodněte.
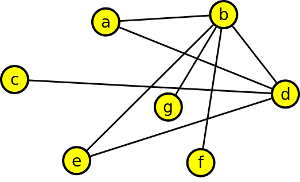
Krok 1
Nejprve vybereme indukovaný podgraf {c,d,e,f,g} grafu G.
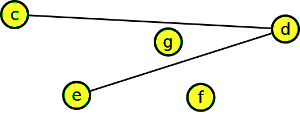
Krok 2
Vytvoříme doplněk grafu.
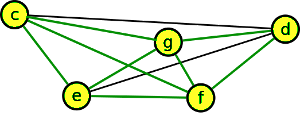
Krok 3
V nakresleném grafu nevidíme ani graf K5, ani K3,3. Můžeme tedy prohlásit, že doplněk grafu je rovinný.
Úlohy k řešení ⇫
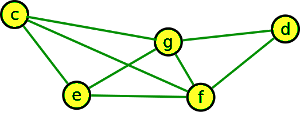
1. Rozhodněte, které z níže uvedených grafů jsou rovinné, a které nikoli?
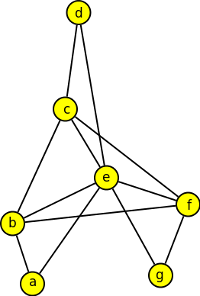
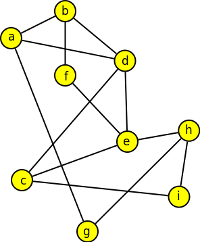
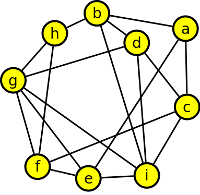
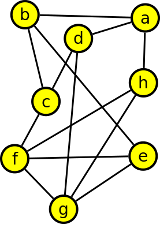
Výsledek
ano, ano, ne - obsahuje K5, ne - obsahuje K3,3
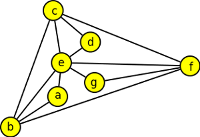
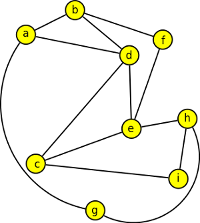
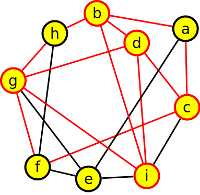
2. Pro která n je graf Kn rovinný? Zdůvodněte.
Výsledek
pro 1 ≤ n ≤ 4, užitím Kuratowského věty
3. Pro která m, n je graf Km,n rovinný?
Výsledek
pouze pro m < 3 nebo n < 3
4. Existuje rovinné nakreslení pro K6 − C3 ? Zdůvodněte.
Výsledek
ne, podle Kuratowského věty
5. Nakreslete nějaký rovinný graf s 21 hranami a 16 stěnami.
Výsledek
Takový graf neexistuje.
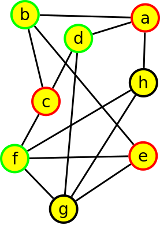
6. Uveďte definici rovinného grafu a rozhodněte, zda následující graf je nebo není rovinný. Své rozhodnutí zdůvodněte.
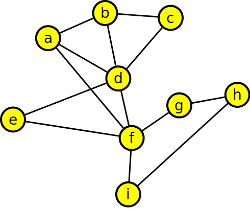
Výsledek
Rovinný graf je takový graf, který můžeme nakreslit do roviny tak, že se žádné jeho hrany vrájemně nekříží.
Tento graf je rovinný, protože žádný jeho podgraf není graf K3,3 ani K5, ani libovolné podrozdělení techto grafů.
Zdroje textů
- DIMA - diskrétní matematika, http://oliva.uhk.cz
- Hliněný, Petr. Diskrétní Matematika (456-533 DIM), 2006
- Kovář, Petr. DISKRÉTNÍ MATEMATIKA a ÚVOD DO TEORIE GRAFŮ ( příklady k procvičení ), 2012
- Wikipedia, http://cs.wikipedia.org/wiki/Platónské_těleso