Hamiltonovské grafy
Teorie ⇫
Definice hamiltonovského grafu a hamiltonovské kružnice:
Hamiltonovskou cestou v grafu nazýváme cestu, která obsahuje všechny vrcholy daného grafu.
Graf, ve kterém existuje kružnice procházející všemi jeho vrcholy právě jednou, nazýváme hamiltonovský graf a příslušnou kružnici hamiltonovská kružnice.
Název grafu se vztahuje ke jménu irského matematika Sira Williama Rowana Hamiltona, který vymyslel v roce 1857 hru, skládající se z pravidelného 12-ti stěnu (obr.1) a 20-ti kolíků. Každý kolík byl umístěn v jednom rohu 12-ti stěnu (tj. v každém vrcholu) a byl označen jménem důležitého hlavního města Evropy. Úkolem hráče bylo najít cestu procházející všechna města, každé právě jednou, a vrátit se zpět do města, z kterého vyšel. Pro přehlednost byl na každém kolíku provázek, který hráč spojil vždy s následujícím kolíkem, v pořadí, jakým města procházel.
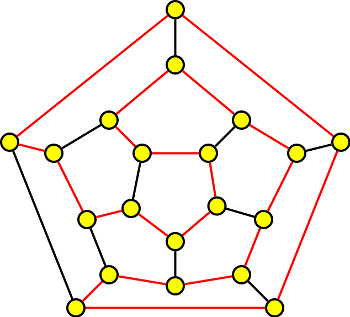
Obr.1 Hamiltonovský graf
Příklady grafů, které nejsou hamiltonovské:
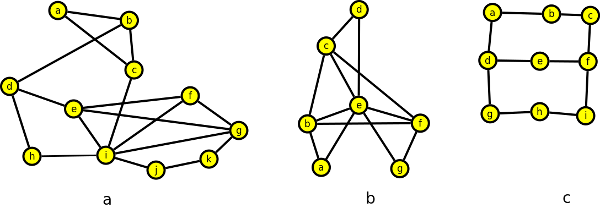
Příklady grafů, které jsou hamiltonovské:
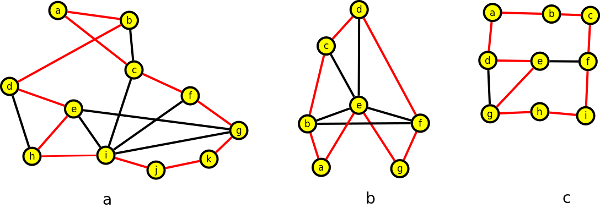
Rozhodnout, zda je graf hamiltonovský, není vždy snadné. Dosud totiž není známa žádná jednoduchá nutná a postačující podmínka k tomu, aby graf byl hamiltonovský. Je známo několik postačujících podmínek k hamiltonovskosti grafu:
- Věta 1 (Dirac, 1952):
Nechť graf G je n-vrcholový, n≥3, stupeň každého vrcholu je alespoň , pak G je hamiltonovský.
- Věta 2 (Ore, 1960):
Nechť G je n-vrcholový graf, n≥3, a nechť pro každou dvojicí nesousedních vrcholů u a v platí: degGu+degGv≥n,pak G je hamiltonovský.
Nutnou podmínku dává následující věta:
- Věta 3:
Nechť G=(V,E) je hamiltonovský graf, S nechť je neprázdná vlastní podmnožina vrcholové množiny V a nechť c(G-S) je počet komponent grafu G-S, pak platí: c(G-S)≤|S|.
Graf G je hamiltovský, hamiltonovka je v grafu vyznačená barevně.
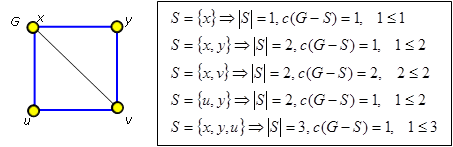
- Důsledek:
Graf Kr,s je hamiltonovský právě tehdy, když r = s.
Poznámka: Opačné tvrzení k Větě 3 neplatí. Viz následující příklad.
Petersenův graf není hamiltonovský, i když pro každou jeho podmnožinu S množiny jeho vrcholů platí tvrzení z Věty 3.
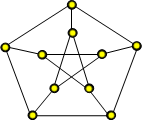
Poznámka: Větu 3 můžeme použít jenom k důkazu, že graf není hamiltonovský. Když najdeme v grafu jedinou vlastní podmnožinu vrcholů, pro kterou neplatí vztah z Věty1, tak můžeme prohlásit, že graf není hamiltovoský. Když pro všechny vlastní podmnožiny platí vztah z Věty1, tak graf může i nemusí být hamiltonovský.
Základní typ algoritmu pro hledání hamiltonovské cesty:
Vezmeme cestu x0, x1, …, xk ve zkoumaném grafu, kterou se pokoušíme prodloužit na hledanou cestu nebo kružnici postupným přidáváním hran vedoucích z koncového vrcholu do ještě nepoužitých vrcholů. Pokud takové prodloužení neexistuje, zkrátíme cestu x1, …, xk a snažíme se prodloužení určit jiným způsobem. Výpočet končí ve chvíli, kdy je buď nalezeno požadované řešení, nebo se neúspěšně proberou všechny možnosti prodlužování.
Typy hamiltonovských úloh
Úlohy, ve kterých jde o hamiltonovské pojmy, mají mnoho variant a lze je třídit z několika různých hledisek. Rozlišujeme existenční a optimalizační úlohy. V existenčních úlohách jde o zjištění existence nebo dokonce o nalezení hamiltonovské cesty, kružnice nebo cyklu v daném grafu. V optimalizačních úlohách jsou hrany grafu ohodnoceny délkami a požaduje se nalezení hamiltonovské cesty, kružnice nebo cyklu o nejmenší délce. Dále úlohy dělíme na orientované a neorientované podle toho, zda hledáme orientovanou nebo neorientovanou hamiltonovskou cestu, případně zda hledáme hamiltonovský cyklus nebo kružnici. V případě hamiltonovských cest musíme navíc rozlišit tři až čtyři varianty podle toho, zda je v zadání úlohy předepsán vrchol, ve kterém musí hamiltonovská cesta začínat, a vrchol, kde musí končit. Všechny výše uvedené typy hamiltonovských úloh jsou pro obecné grafy NP – těžké (tj. neexistuje pro úlohu algoritmus, který by jí řešil v polynomiálním čase).
Uvedeme základní pravidla pro hledání hamiltonovské kružnice v daném malém grafu:
- Má-li daný graf n vrcholů, pak hamiltonovská kružnice má právě n hran.
- Jestliže vrchol v má stupeň k, pak hamiltonovská kružnice musí obsahovat právě dvě hrany incidentní s vrcholem v.
- Při konstrukci hamiltonovské kružnice nemůže být vytvořena kružnice, která by neobsahovala všechny vrcholy daného grafu.
- Jakmile hamiltonovská kružnice, kterou konstruujeme, prochází vrcholem v, pak ostatní nepoužité hrany incidentní s vrcholem v můžeme vyloučit (tyto již v hamiltonovské kružnici ležet nebudou).
Příklad
Návštěvy obvodního lékaře
Obvodní lékař potřeboval navštívit všechny své pacienty, ale tak, aby každého pacienta navštívil právě jednou. Situace je zakreslena v následujícím grafu, kde vrcholy grafu jsou pacienti a hrany cesty mezi nimi. Je možno takovou cestu vykonat?
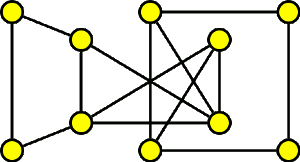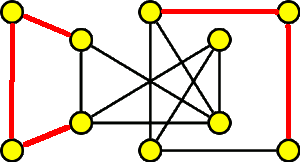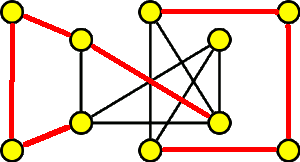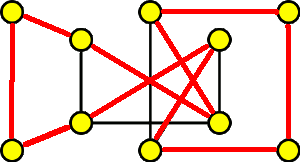
Z animace je zřejmé, že takovou návštěvu vykonat lze. Výsledná návštěva je hamiltonovská kružnice.
Poznámka: Z animace je potrné, že při konstrukci hamiltonovské kružnice postupujeme podle výše uvedených pravidel. Je vhodné začít ve vrcholech stupně 2 a potom postupně obarvovat další hrany až vznikne hamiltonovská kružnice.
Řešený příklad ⇫
1. Rozhodněte, zda následující graf obsahuje hamiltonovskou kružnici, či nikoli.
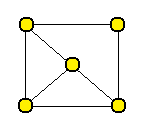
Krok 1
Při rozhodování, zda je graf hamiltonovský musíme podle základních pravidel najít hamiltonovskou kružnici. Z následujícího obrázku vidíme, že graf hamiltonovský je i když nesplňuje Větu 1 (obsahuje vrchol 2. stupně, přičemž 2<5/2)
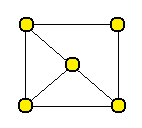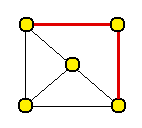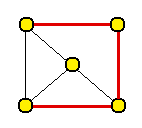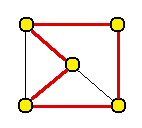
Krok 2
Splňuje Větu 2 (součet stupňů libovolných dvou nesousedních vrcholů je alespoň 5). Je tedy podle výše uvedených podmínek hamiltonovský.
Z uvedeného jasně vidíme, že Věty nejsou nutné podmínky pro určování hamiltonovských grafů.
2. Rozhodněte, zda následující graf je hamiltonovský?
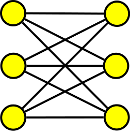
Krok 1
Podle základních pravidel najdeme v grafu hamiltonovskou kružnici.
Krok 2
Hamiltonovská kružnice je na následujícím obrázku:
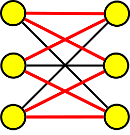
Krok 3
Tentokrát graf splňuje všechny tři věty.
Úlohy k řešení ⇫
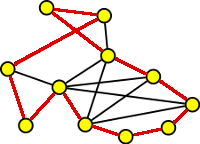
1. Najděte v grafech na obrázku hamiltonovskou kružnici (existuje jich více).
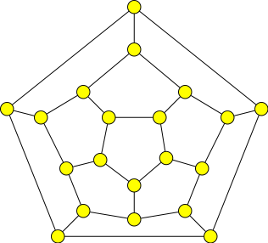
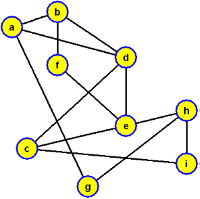

Výsledek
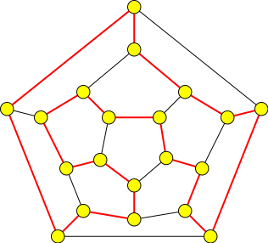
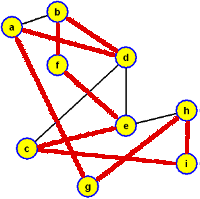
2. Dokažte sporem tvrzení:
Jestliže v grafu G existuje most, pak v grafu G neexistuje hamiltonovská kružnice. (nejprve správně zformulujte tvrzení pro důkaz sporem!)
Výsledek
Důkaz sporem:
Nechť předpoklad neplatí: V grafu G existuje most a zároveň v grafu existuje hamiltonovská kružnice.
V G existuje hamiltonovská kružnice ⇒ v G existuje kružnice C obsahující všechny vrcholy. Hrany grafu můžeme rozdělit do dvou skupin E1, E2. Skupina E1 - hrany ležící na kružnici C, E2 - hrany neležící na kružnici C.
Podle věty: Jestliže hrana e∈E leží na kružnici, pak hrana e není most. Žádná hrana e∈E1 není most.
A když z grafu odebereme libovolnou hranu e∈E2, tak v G-e existuje kružnice C, obsahující všechny vrcholy grafu ⇒ pro všechny libovolné dva vrcholy existuje cesta (po kružnici) ⇒ G-e je souvislý, proto žádná hrana e∈E2 není most.
Tedy graf G neobsahuje most a to je spor s předpokladem, proto platí původní tvrzení.
Zdroje textů
- DIMA - diskrétní matematika, http://oliva.uhk.cz
- Hliněný, Petr. Diskrétní Matematika (456-533 DIM), 2006
- Kovář, Petr. DISKRÉTNÍ MATEMATIKA a ÚVOD DO TEORIE GRAFŮ ( příklady k procvičení ), 2012
- Wikipedia, http://cs.wikipedia.org/wiki/Hamiltonovský_graf