DIMA - Teorie grafů



Procházení labyrintu

Teorie ⇫

Stavba labyrintů je starověké umění, vzpomeňme jen řeckou báj o Ariadnině niti, která bezpečně vyvedla Thésea z krétského labyrintu.

Nejen klubko niti, ale též například jednoduché pravidlo „pravé ruky“ nás bezpečně dostane zpět k místu, odkud jsme začali bludiště procházet. Například vstoupíme-li do „živého“ bludiště v zahradě Hampton Court, které je reprezentováno nákresem na Obrázku 1 (převzato z [1]) a použijeme-li některý z výše uvedených postupů, tak se bezpečně dostaneme ven z bludiště, ale obecně těmito přístupy k procházení bludiště nemáme zaručeno, že ho projdeme celé.

labyrint

Obrázek 1

V praxi však velmi často potřebujme projít celý daný úsek (zkontrolovat v nějaké části města chodníky, zda jsou v zimě uklizené; systematicky projít celou zoologickou zahradou; naplánovat si trasu výletu apod.) Příkladů na tuto problematiku je mnoho.

Přestože konstrukce labyrintů je starověké umění a problémy související s otázkou, jak se z labyrintu dostat ven, zajímaly lidi jistě již od pradávna, seriózní pohled na tuto problematiku byl započat až koncem 19 století. V práci [1] se můžeme dočíst, že první pokus o formulaci algoritmu, týkajícího se procházení labyrintem, podal v roce 1873 Wiener, ale jeho přístup byl zbytečně komplikovaný a neefektivní, že mnohem efektivnější algoritmus, který umožňuje projít celý labyrint a vrátit se zpět, navrhl a v roce 1882 publikoval francouzský matematik Trémaux, a že v roce 1895 Gaston Tarry, též francouzský matematik, popsal ještě jednodušší, obecné řešení této úlohy.

Dříve než se věnujeme algoritmům, které popisují průchod labyrintem, ukážeme na příkladu labyrintu v zahradě Hampton Court, jak lze libovolný labyrint transformovat do podoby grafu.

Obrázek labyrintu (Obrázek 1) nejprve doplníme písmeny tak, aby byly vyznačeny konce chodeb a křižovatky, tj. místa, kde se chodby setkávají, a pak jej jednoduše převedeme na graf tak, že písmena reprezentují vrcholy a chodby mezi nimi hrany (viz Obrázek 2 a Obrázek 3 převzaté z [1]).

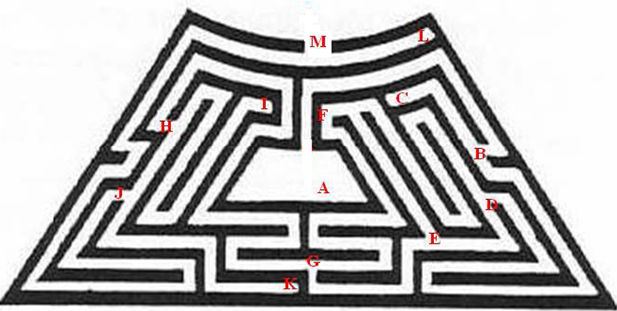
labyrint

Obrázek 2

labyrint

Obrázek 3

Nyní zformulujeme algoritmy, které popisují průchod celým labyrintem, každou chodbou v obou směrech (tam a zpět) právě jednou. Namísto pojmů chodba a křižovatka použijeme pojmy vrchol a hrana.

Trémauxův algoritmus

  1. Každou hranou smíme projít v jednom směru nejvýše jednou.
  2. Po hraně, po které jsme do vrcholu přišli poprvé, se můžeme vracet pouze tehdy, nemáme-li jinou možnost.
  3. Jestliže přijdeme hranou, procházenou poprvé, do známého vrcholu, tak se hned v následujícím kroku touto hranou vracíme zpět.

Tarryho algoritmus

  1. Každou hranou smíme projít v jednom směru nejvýše jednou.
  2. Po hraně, po které jsme do vrcholu přišli poprvé, se můžeme vracet pouze tehdy, nemáme-li jinou možnost.

Tarry nejen dokázal správnost svého řešení, ale navrhl i způsob, jak si při průchodu labyrintem počínat:

  • Chodbu procházenou poprvé označíme na jejím začátku dvěma značkami a na jejím konci jednou nebo třemi značkami v závislosti na tom, zda chodba vede k již navštívené křižovatce (jednu značku) nebo ke křižovatce dosud nenavštívené (tři značky). Při vstupu do chodby, kde je pouze jedna značka (tj. půjdeme touto chodbu podruhé, ale samozřejmě v opačném směru), přidáme k této značce druhou značku.
  • K pokračování z křižovatky si náhodně vybereme chodbu, která nemá ještě značení nebo chodbou s jedním značením. Pokud žádná taková neexistuje, pokračujeme chodbou se třemi značkami.

Průchod labyrintem Trémauxovým přístupem s použitím uvedeného značení můžeme formulovat obdobně (první odstavec je shodný):

  • Chodbu procházenou poprvé označíme na jejím začátku dvěma značkami a na jejím konci jednou nebo třemi značkami v závislosti na tom, zda chodba vede k již navštívené křižovatce (jednu značku) nebo ke křižovatce dosud nenavštívené (tři značky). Při vstupu do chodby, kde je pouze jedna značka (tj. půjdeme touto chodbu podruhé, ale samozřejmě v opačném směru), přidáme k této značce druhou značku.
  • Pokud značíme konec chodby jednou značkou, přidáme k této značce druhou značku a vracíme se ihned touto chodbou zpět. K pokračování z křižovatky, ke které jsme přišli poprvé, vybereme chodbu, která nemá ještě značení. Pokud žádná taková neexistuje, pokračujeme chodbou se třemi značkami.

    Pozn.: Je zřejmé, že při uvedeném způsobu značkování vždy platí:

    • Do chodby označené dvěma značkami (tou jsme již prošli v obou směrech) nevstupujeme.

    Pozn.: Skutečnost, že jsme nějakou křižovatku již navštívili, si můžeme představit např. tak, že jsme v té křižovatce rozsvítili svíčku, lampu apod.

Na první pohled je patrné, že algoritmy se liší pouze v jediném bodě. Tarryho algoritmus je obecný, Trémauxův algoritmus je jeho speciálním případem.

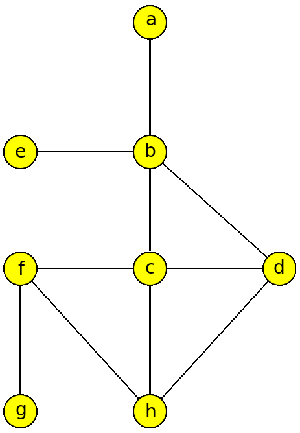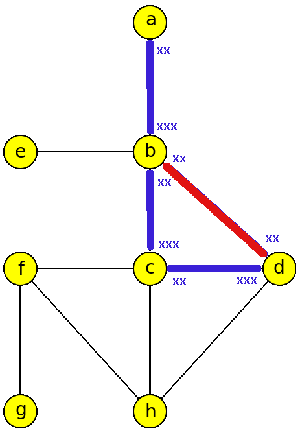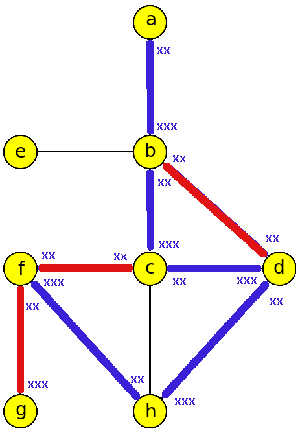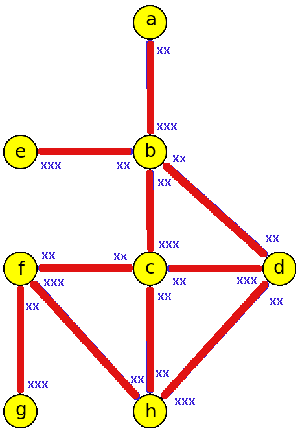
Trémaux

Trémaxův algoritmus procházení labyrintem

Tarryho přístup k prohledávání labyrintů inspiroval v roce 1973 Edmondse a Johnsona k formulaci dalšího speciálního případu procházení labyrintem.

Edmonds-Johnson algoritmus

  1. Každou hranou můžeme projít v jednom směru nejvýše jednou.
  2. Po hraně, po které jsme do vrcholu přišli poprvé, se můžeme vracet pouze tehdy, nemáme-li jinou možnost.
  3. Z hran, které máme k odchodu z vrcholu k dispozici, upřednostňujeme tu hranu, kterou jsme dosud nikdy nešli.

V terminologii výše uvedeného značení použitého při průchodu labyrintem můžeme Edmonds-Johnsonův přístup formulovat následovně (první část je opět shodná):

  • Chodbu procházenou poprvé označíme na jejím začátku dvěma značkami a na jejím konci jednou nebo třemi značkami v závislosti na tom, zda chodba vede k již navštívené křižovatce (jednu značku) nebo ke křižovatce dosud nenavštívené (tři značky). Při vstupu do chodby, kde je pouze jedna značka (tj. půjdeme touto chodbu podruhé, ale samozřejmě v opačném směru), přidáme k této značce druhou značku.
  • K pokračování z křižovatky si vybereme chodbu, která nemá ještě značení. Pokud žádná taková neexistuje, pokračujeme chodbou s jedním značením. Pokud ani žádná taková chodba neexistuje, pokračujeme chodbou se třemi značkami.

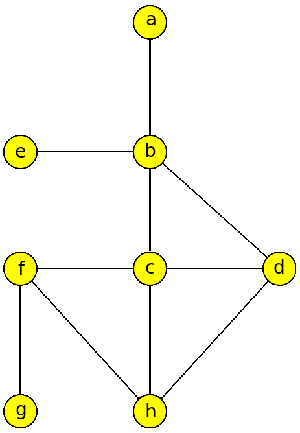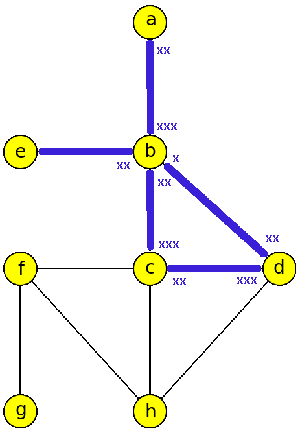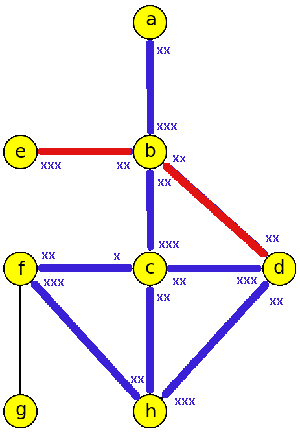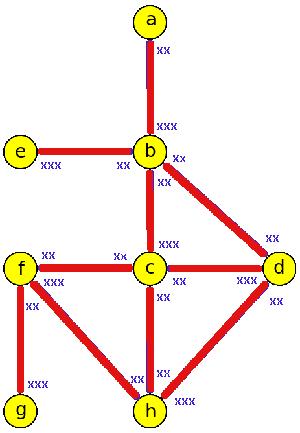
Edmonds-Johnson

Edmonds-Johnsonův algoritmus procházení labyrintem

Příklad

Přes noc nasněžilo a úkolem je odklidit sníh z chodníků v ulicích jisté části města, jehož plánek máme k dispozici (viz graf níže). Jedná se o ulice, které mají chodníky po obou stranách. Jak je potřeba naplánovat úklid, aby průchod ulicemi byl efektivní (tj. abychom každou stranu ulice prošli právě jednou)?

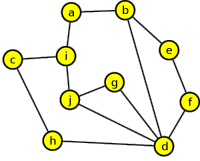
Mapa města

Řešení ilustrujeme nejprve pomocí Trémauxova algoritmu, pak pomocí Edmonds-Johnsonova algoritmu. Namísto křížkování využijeme práci s datovou strukturou zásobník (LIFO).

Abychom zajistili vlastnost Trémauxova algoritmu - jestliže přijdeme hranou, procházenou poprvé, do známého vrcholu, tak se hned v následujícím kroku touto hranou vracíme zpět - uložíme do zásobníku každý vrchol právě jednou, a to pouze v okamžiku, když do vrcholu vstoupíme poprvé. Naopak, v případě Edmonds-Johnsonova algoritmu ukládáme do zásobníku každý vrchol pokaždé, když do něj vstoupíme.

Poznámka: Zásobník (nebo-li LIFO, zkratka pro anglické vyjádření Last-In-First-Out) je speciální název pro datovou strukturu, se kterou se provádí tři operace se seznamy (posloupnostmi prvků):

  • určení posledního prvku seznamu
  • přidání nového prvku za poslední prvek seznamu
  • odebrání posledního prvku seznamu

V následujících ilustracích algoritmů zapisujeme hrany grafu v pořadí, jak jimi procházíme při použití jednotlivých algoritmů, přičemž hranu, po které se vracíme, vyznačujeme tučně.

Procházení grafu začneme ve vrcholu a, při procházení, máme-li více možností pokračování, respektujeme lexikografické (abecední) pravidlo.

Ilustrace Trémauxova algoritmu
Do datové struktury LIFO ukládáme vrcholy právě jednou, v pořadí: a,b,d,f,e,g,j,i,c,h
Průchod hranami: {a,b}, {b,d}, {d,f}, {f,e}, {e,b}, {b,e}, {e,f}, {f,d}, {d,g}, {g,j}, {j,d}, {d,j}, {j,i}, {i,a}, {a,i}, {i,c}, {c,h}, {h,d}, {d,h}, {h,c}, {c,i}, {i,j}, {j,g}, {g,d}, {d,b}, {b,a}
Ilustrace Edmonds-Johnsonova algoritmu
Do datové struktury LIFO ukládáme vrchol pokaždé, když do něj vstoupíme, tj. vrcholy jsou uloženy v  pořadí: a,b,d,f,e,b,g,j,d,h,c,i,a,j
Průchod hranami: {a,b}, {b,d}, {d,f}, {f,e}, {e,b}, {b,e}, {e,f}, {f,d}, {d,g}, {g,j}, {j,d}, {d,h}, {h,c}, {c,i}, {i,a}, {a,i}, {i,j}, {j,i}, {i,c}, {c,h}, {h,d}, {d,j}, {j,g}, {g,d}, {d,b}, {b,a}

Řešený příklad ⇫

V následujícím grafu (zadaném obrázkem) určete pořadí hran při prohledávání „Edmonds-Johnsonovým“ algoritmem. Začněte ve vrcholu e a dodržujte lexikografické pravidlo.

Labyrint

Krok 1

Z vrcholu e jdeme do a

krok1

Zapíšeme: ea.

Krok 2

Z vrcholu a jdeme do b

krok1

Zapíšeme: ea,ab.

Krok 3

Z vrcholu b jdeme do e

krok1

Zapíšeme: ea,ab,be.

Krok 4

Z vrcholu e jdeme do d

krok1

Zapíšeme: ea,ab,be,ed.

Krok 5

Z vrcholu d jdeme do a

krok1

Zapíšeme: ea,ab,be,ed,da.

Krok 6

Z vrcholu a jdeme do f

krok1

Zapíšeme: ea,ab,be,ed,da,af.

Krok 7

Z vrcholu f jdeme do b

krok1

Zapíšeme: ea,ab,be,ed,da,af,fb.

Krok 8

Cestu do vrcholu a můžeme použít až jako poslední možnost, protože jsme odtud přišli do b poprve. Proto se vracíme do f

krok1

Zapíšeme: ea,ab,be,ed,da,af,fb,bf.

Krok 9

Z vrcholu f jdeme do e

krok1

Zapíšeme: ea,ab,be,ed,da,af,fb,bf,fe.

Krok 10

Z vrcholu e jdeme do b

krok1

Zapíšeme: ea,ab,be,ed,da,af,fb,bf,fe,eb.

Krok 11

Z vrcholu b jdeme do a

krok1

Zapíšeme: ea,ab,be,ed,da,af,fb,bf,fe,eb,ba.

Krok 12

Z vrcholu a jdeme do d

krok1

Zapíšeme: ea,ab,be,ed,da,af,fb,bf,fe,eb,ba,ad.

Krok 13

Z vrcholu d jdeme do e

krok1

Zapíšeme: ea,ab,be,ed,da,af,fb,bf,fe,eb,ba,ad,de.

Krok 14

Z vrcholu e jdeme do f

krok1

Zapíšeme: ea,ab,be,ed,da,af,fb,bf,fe,eb,ba,ad,de,ef.

Krok 15

Z vrcholu f jdeme do a

krok1

Zapíšeme: ea,ab,be,ed,da,af,fb,bf,fe,eb,ba,ad,de,ef,fa.

Krok 16

Z vrcholu a jdeme do e

krok1

Zapíšeme: ea,ab,be,ed,da,af,fb,bf,fe,eb,ba,ad,de,ef,fa,ae.

Úlohy k řešení ⇫

1. V následujícím grafu (zadaném obrázkem) určíme pořadí hran při prohledávání „Trémaux“ algoritmem. Začneme ve vrcholu e a dodržujeme lexikografické pravidlo.

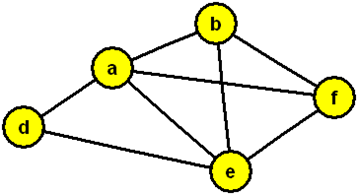
příklad

Výsledek

Hrany: ea, ab, be, eb, bf, fa, af, fe, ef, fb, ba, ad, de, ed, da, ae

2. Projděte graf výše Edmonds-Johnsonovým algoritmem a vypište pořadí hran.

Výsledek

Hrany: ab, be, ea, ad, de, ef, fa, ae, ed, da, af, fe, eb, ba

3. V následujícím grafu určete pořadí hran při prohledávání "Trémaux" algoritmem. Začněte ve vrcholu b a dodržujte lexikografické pravidlo.

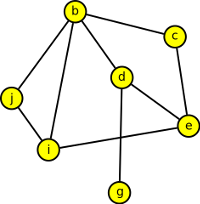
Labyrint

Výsledek

Hrany: bc, ce, ed, db, bd, dg, gd, de, ei, ib, bi, ij, jb, bj, ji, ie, ec, cb.

4. Představte si, že následující graf reprezentuje jistou část města (vrcholy = křižovatky, hrany = ulice). Vaším úkolem je optimálním (co nejkratším) způsobem projít všechny ulice a zjistit, na kolika zvoncích je napsáno jméno Novák (Nováková, Novákovi). Ohodnocení hran reprezentuje délku jednotlivých ulic (ulice jsou různě „zakroucené“)

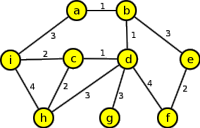
Mapa města

Výsledek

Ze zadání úlohy je zřejmé, že musíme projít každou ulici a to po každém chodníku (každá strana ulice). Proto na řešení použijeme průchod labyrintem. Délky ulic nemusíme tedy vůbec brát v úvahu.

Při průchodu Trémauxovým algoritmem dostaneme pořadí ulic: ab, bd, bc, ch, hd, dh, hi, ia, ai, ic, ci, ih, hc, cd, df, fe, eb, be, ef, fd, dg, gd, db, ba.

Při průchodu Edmonds-Johnsonovým algoritmem dostaneme pořadí následující: ab, bd, dc, ch, hd, df, fe, eb, be, ef, fd, dg, gd, dh, hi, ia, ai, ic, ci, ih, hc, cd, db, ba.

Zdroje textů

  1. Biggs, N. L., Lloyd, K. E., Wilson, R. J.. Graph theory 1736-1936. Clarendon Press, Oxford, 1976
  2. DIMA - diskrétní matematika, http://oliva.uhk.cz
  3. Soukal, Muhl. Soukal_Muhl_labyrinty.ppt, http://oliva.uhk.cz/webapps/blackboard/execute/content/file?cmd=view&content_id=_92599_1&course_id=_296_1
  4. Hliněný, Petr. Diskrétní Matematika (456-533 DIM), 2006
  5. Kovář, Petr. DISKRÉTNÍ MATEMATIKA a ÚVOD DO TEORIE GRAFŮ ( příklady k procvičení ), 2012